Optimised excessive gradient boosting mannequin for brief time period electrical load demand forecasting of regional grid system

Loading forecasting dataset and information exploring

Île-de-France (actually “Isle of France”) is among the 13 administrative areas in mainland France and the capital circle of Paris. The common temperature is 11 °C, and the typical precipitation is 600 mm. Île-de-France is probably the most densely populated area of France. In response to the 2019 report, this area offers France with 1 / 4 of jobs in whole employment, of which the tertiary sector accounts for close to nine-tenths of jobs. Agriculture, forests and pure areas cowl almost 80% of the floor. As nicely, the area, as the primary industrial zone in France, contains electronics and ICT, aviation, biotechnology, finance, mobility, automotive, prescription drugs and aerospace.

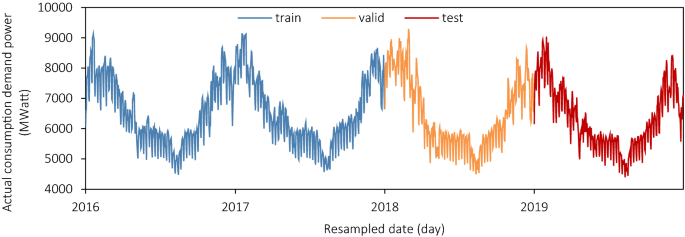
We analysed the facility load within the Île-de-France area with a 30-min sampling charge with a complete of 70,128 information over 4 years, from 2016 to 2019. The information is from the éCO2mix API offered by the RTE (Réseau de Transport d’Électricité)¹⁵. The unique information had been resampled as the utmost each day energy into 1461 information in Fig. 1, whose y-axis is the real-time demand load energy (unit: MWatt). As proven beneath, the development between the years of the collection is analogous and has an evident periodicity; every cycle is V-shaped with seen seasonality. Because of the traits of energy load and the area’s precise state of affairs, every cycle’s development is steady with out an obvious progress or decay.

Demand consumption {of electrical} energy (each day, MWatt).

The dataset we collected from éCO2mix is split into three elements, the blue coaching dataset (2016, 2017), the orange validation dataset (2018) and the pink testing dataset (2019) in Fig. 1. The coaching one builds the principle fashions, and the validation one is analysed for optimisation eval. And testing one will test the fashions’ efficiency on a number of completely different metrics. The information exploring a part of the time collection will likely be completed within the validation one in 2018 to keep away from information leakage.

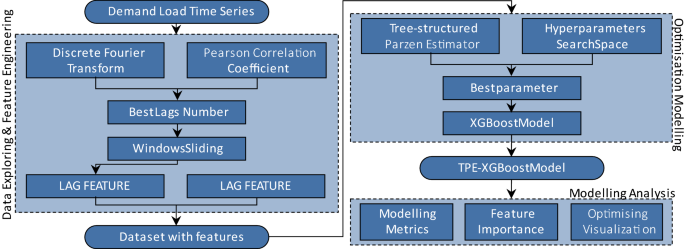
Within the following Desk 1, we use characteristic engineering to rework time collection right into a supervised studying dataset for machine studying as the extra date characteristic¹⁶.

Lastly, loading forecast values on the first N moments will likely be added to the dataset as a reminiscence characteristic within the type of a sliding window referred to as momery_feature_1 ~ momery_feature_N. Nevertheless, the selection of N, the reminiscence size or the time lag just isn’t informal. We are going to use a technique combining Discrete Fourier Rework and Pearson Correlation Coefficient to finish the reminiscence size willpower.

The perfect width of home windows evaluation

Knowledge-driven hundreds forecasting problems with machine studying require the datasets to be produced within the type of sliding home windows. Then, the time collection challenge transforms right into a supervised regression in machine studying. And there’s a complicated impact on the window width or referred to as lags rely of the dataset. The longer width of the window, the extra considerable the reminiscence data as extra options within the pattern. Nevertheless, for the machine studying algorithms based mostly on statistics expertise, extra options would trigger unideal outcomes for sensible software by too many irrelevant options. Alternatively, too brief a window means fewer options, which could be underfitting for inadequate data.

Determine 2 above is the impact of various window widths within the testing dataset of the XGBoost mannequin and Linear Regression (OPLS), whose x-axis is the window’s width of knowledge options and the y-axis is the imply absolute error (models: MWatt) within the testing dataset (2019), and the fashions listed 1 imply no date options including. It may be seen that the connection between the efficiency and window width just isn’t a easy linear relationship. This determine exhibits a dramatic decline in MAE with wider home windows, it reached a low level, after which the MAE fluctuates inside a particular vary and worsens when the home windows widen.

MAE metrics with wider home windows of testing dataset.

The Fourier Rework is a sensible software for extracting frequency or periodic elements in sign evaluation. Typically, the artificial sign (fleft(tright)) will be transformed to frequency area part indicators (g(freq)) as beneath if it satisfies the Dirichlet situations within the vary of ((-infty ,+infty )):

the facility hundreds time collection on this paper are sampled discretely with restricted size, and the Quick Discrete Fourier technique proposed by Bluestein¹⁷ is used as a substitute as beneath:

the place (N=365) is from the validation dataset in 2018, and the (freq) collection include the frequency bin facilities in cycles per unit of the pattern spacing with zero firstly. The second half of (freq) collection is the conjugate of the primary half, solely the constructive is saved. And produce (interval=frac{1}{freq}) again as beneath:

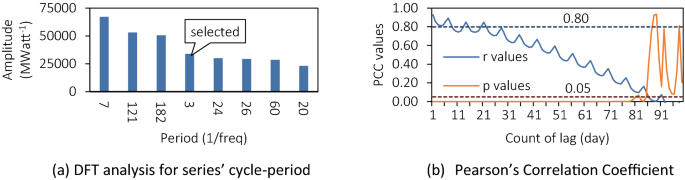
Take away the (inf) and the (interval=N) merchandise (g(interval)), and the primary eight amplitude of (period-gleft(periodright)) bar plots as proven in Fig. 3a¹⁸. A few of the intervals are associated to the pure time cycle: 121 as 1 / 4 of a yr, 182 as a semi-annual. And never all the that means is obvious, similar to 3, 24 and 26, that are tough to have adequate clarification.

Options engineering of home windows width evaluation.

Additional, the Pearson correlation coefficient (PCCs) are used to calculate a extra detailed interval. The PCCs measure the linear relationship between two datasets as beneath:

the place the ({varvec{x}}({t}_{0})) is the collection to foretell as y goal of dataset and the ({varvec{x}}left({t}_{0}-delta proper)) is the (delta ) lag collection of ({t}_{0}). The bigger PCC means there are extra correlated relationships between two collection.

In Fig. 3b, the X-axis is the time interval numbers and the Y-axis is the Pearson’s Correlation Coefficient values (blue) and Two-tailed p-value (orange). In response to expertise within the normal statistical sense¹⁹, when the Pearson Coefficient is bigger than 0.80 (blue dotted line), it may be thought of that the 2 collection have a robust correlation; when the p-value is lower than 0.05 (orange dotted line), the speculation is established. The orange curve exhibits that the about first 50 reminiscence options have a constructive correlation with the anticipated goal, so the minimal interval must be lower than 50. Moreover, Reminiscence-feature 1 ~ 5 have Pearson’s correlation coefficient values higher than 0.80; that’s, the values inside 5 are strongly correlated. And the variety of intervals within the FFT to fulfill this worth requirement is 3, subsequently, our mannequin will use 3 because the window width.

We are going to additional examine the three sorts of widths, 7, 14 and 28, as a management to finish the sequential modelling.

Excessive gradient boosting optimised by tree-structured Parzen estimator

Gradient Boosting originates from the paper by Friedman in 2011²⁰. XGBoost is an open-source software program library of utmost gradient boosting developed by CHEN Tianqi²¹ that ensembles tree fashions by a collection of methods and algorithms similar to a grasping search technique based mostly on gradient boosting. As an additive ensemble mannequin, XGBoost considers the gradient of first-order by-product and second-order by-product within the Taylor collection for the loss operate and constructs within the case of chance roughly right (PAC). The target operate is as follows:

the place the (t) means the rounds of ensemble processing and the (omega ) means the regularisation half.

Take a second-order Taylor enlargement on the loss operate and add the parameters of the tree construction within the common time period, Then the target operate transforms into beneath:

the place the (g) and the (h) is the by-product time period of the loss operate; the (T) and (omega ) are the parameters of ensembled resolution timber’ construction parameters; (gamma ) is the minimal loss required for additional partitioning on the leaf nodes of single tree; (lambda ) is the L2 regularization time period.

A grasping technique to solves the (obj(t)) for an area optimum resolution (upomega =-frac{G}{lambda +mathrm{H}}) then Deliver again:

With the meta, weak learner (t) generated in every spherical, (bes{t}_{objleft(tright)}) is used because the basement technique for the expansion of the choice tree, which controls the generalisation potential for the boosting course of.

Most particular element for XGBoost can discuss with the paper, XGBoost: A scalable tree boosting system²¹.

XGBoost is a robust ensemble algorithm, and there are quite a few hyper-parameters to tune for the most effective efficiency in software, nevertheless, it’s a black-box course of extensively recognised²². We undertake the Tree-structured Parzen Estimator²³ (TPE), one of many sequential model-based optimisation strategies (SMBO) based mostly on the Bayesian theorem, to optimise our XGBoost mannequin for time-series forecasting. The TPE pseudocode as beneath proven in Fig. 4:The place the ({varvec{z}}) is the set of hyperparameters of the search house, the (s) is the metrics rating of XGBoost with ({varvec{z}}) within the validation dataset, and the (H) is the historical past of validation scores and the chosen ({varvec{z}}).

Pseudocode of Tree-structured Parzen Estimator optimising XGBoost.

The EI is the core of TPE, which builds a chance mannequin of the target operate and makes use of it to pick probably the most promising hyperparameters to judge within the true goal operate²³:

the (l({varvec{z}})) is the worth of the target operate lower than the brink (ok), and (g({varvec{z}})) is the target operate higher than the brink.

We first construct the XGBoost mannequin (XGBoost) by default values in Desk 2, after which 9 hyper-parameters in Desk 2 are going to be optimized within the looking house beneath by the TPE algorithm for TPE-XGBoost fashions.

Alpha: a regularization parameter in meta learners’ ensemble; Lowering it can give mannequin looser constraints. And that is the one hyperparameter on this paper to manage mannequin within the ensemble degree by regularization.

Studying charge: a weight parameter for brand new meta learners to decelerate the boosting ensembles; smaller studying charge would make ensemble slower however extra conservative.

Max depth of single tree: a parameter of meta fashions struction; deeper tree would extra complicated however extra probably overfitted.

Minimized youngster weight: a parameter of meta fashions struction by controlling leaf nodes. If a leaf node with the sum of occasion weight lower than it, the node will likely be given up as a leaf; Too small weight would make ensembled mannequin straightforward to underfit.

Minimized break up loss: a parameter for meta fashions constructing by leaf nodes building. The nodes can be deserted if the loss lower than this parameter; The bigger it’s, the extra conservative the algorithm can be.

Subsample: it’s samples counts ratio of subset for coaching; A balanced Subsample can forestall overfitting, however too small subsample would make fashions exhausting to fulfill software.

Col pattern by tree/degree/node: it’s a subsample for options as Subsample above did.

We restrict the tuning iterations to 500 and the goal of every iteration will likely be set of the MAPE within the validation dataset (2018). And the Fig. 5 is the entire circulation course of on this paper.

Function Engineering and Optimised Modelling Course of.