Enumeration optimization of open pit manufacturing scheduling primarily based on cellular capability search area

The manufacturing capability, mining sequence and mining lifetime are the three important elements within the optimization of open pit mine manufacturing scheduling. Whereas manufacturing capability is expounded to technical situations of the mine, mining sequence is expounded to mine group administration, and mining lifetime is restricted by mine scheduling and business norms; moreover, these three elements are affected by geological situations of the ore physique, reserves scale, advertising and marketing setting and different components^1,2,3,4. As well as, in contrast with different exterior situations, there may be additionally interplay and affect among the many three components of manufacturing scheduling. For instance, the extra important the manufacturing capability is, the shorter the mining productive life. Completely different mining sequences (pit development place on the finish of the yr) straight have an effect on the yr’s manufacturing capability after which have an effect on the general mining life. In follow, subsequently, optimized mining scheduling determines the annual estimated quantity of mined ore, the annual estimated quantity of stripped waste rock (i.e., manufacturing capability), which areas are mined and stripped every year or how every step is superior (i.e., the mining sequence), and the mining interval (i.e., the mining lifetime).

Manufacturing scheduling gives a future manufacturing technique for a mine (new mine or mine in producing). Furthermore, for a given deposit, the standard of the manufacturing schedule has a big impression on infrastructure funding and money movement, which is distributed on the timeline after manufacturing. This affect turns into an vital issue within the funding return charge of the entire mine challenge. That’s the reason worldwide mining firms have a robust curiosity in optimizing manufacturing scheduling. Manufacturing scheduling optimization is all the time a preferred analysis subject in mine system engineering. From the angle of optimization, the open pit mine manufacturing schedule determines the mining time of every module within the huge deposit mannequin to find out which module ought to be mined every year to maximise the whole NET current worth and meet the area–time relationship and technical and financial constraints of open pit mining.

The “mining increment sorting technique” is the earliest pc optimization technique utilized to manufacturing scheduling. It was first proposed by engineers of the Kennecott Firm and utilized within the firm. The mining increment is generated by establishing cones, and cone construction, analysis and sequencing are carried out by way of human–pc interplay trial and error⁵. Manufacturing increments for manufacturing scheduling will be obtained by the “parametric evaluation” proposed by Lerchs and Grossmann⁶. This technique is additional developed into the “reserve parameterization” technique, and plenty of students have carried out additional analysis on the answer of reserve parameterization and its utility in manufacturing scheduling^{7,8,9,10,11,12}.

One of many inherent defects of parameterization is the “notch” drawback; within the generated restrict sequence, the increments between among the adjoining limits are so giant that the restrict sequence can’t be used for manufacturing scheduling optimization. Due to this fact, some researchers use heuristic algorithms to generate nested restrict sequences to beat the hole drawback^{13,14,15,16,17,18,19,20} and dynamically order the ensuing restrict sequence^{18,21,22,23,24,25}.

In abstract, the essence of the manufacturing scheduling optimization drawback is to find out the optimum manufacturing time of every module on the premise of assembly the mandatory constraint situations to acquire the utmost complete NET current worth. It’s a typical linear programming drawback. Due to this fact, linear programming (its particular type contains combined programming, pure integer programming and 0–1 programming) is among the mostly used mathematical optimization strategies to resolve the optimization drawback of manufacturing scheduling; associated research had been carried out as early because the late Nineteen Sixties ^26,27. Many researchers have established linear programming fashions with completely different concrete varieties for various features of manufacturing scheduling issues^{27,28,29,30,31,32,33,34,35}.

Nonetheless, the amount of variables and constraint equations within the linear programming mannequin for optimizing manufacturing scheduling is simply too monumental when a single module within the huge deposit mannequin is used as the choice unit. That could be a state of affairs that even as we speak’s computer systems can’t resolve straight; whether it is integer programming, it might probably hardly be solved. Due to this fact, some researchers attempt to discover options within the development of mathematical mannequin varieties (primarily constraints) or fixing algorithms (normally by feat of approximate algorithms) to spice up the fixing velocity^{36,37,38,39,40,41,42}. Rising the decision-making unit to cut back the amount of variables and constraints is a extra frequent means, comparable to combining the modules within the deposit mannequin right into a “unit tree” as the choice unit in optimization or taking steps or panels as the choice unit^{37,43,44,45,46,47,48,49,50,51}. Nonetheless, because of the low scheduling accuracy (or decision) in monumental choice items, the outcomes are considerably completely different from the optimum plans, which additionally reduces the practicality of the outcomes^47,49,52,53. Due to this fact, many researchers make use of the distinctive construction of the mathematical mannequin to cut back the mannequin dimension with the Lagrange leisure technique and resolve the mannequin with different measures and algorithms, comparable to iteration, decomposition, gradient technique, and the Dantzig community movement technique^{54,55,56,57,58,59,60,61,62,63,64,65,66,67,68}. The largest impediment to this method is the “hole” drawback. Researchers have tried varied strategies to resolve this drawback, however they haven’t sought out appropriate means.

Open pit mine manufacturing scheduling is a typical multi-period decision-making drawback; furthermore, the time is interrelated in order that dynamic programming can be utilized to resolve it. Due to this fact, dynamic programming can also be some of the used mathematical optimization strategies to resolve the issue. Researchers have used dynamic programming to review the optimization of various features of manufacturing scheduling^{1,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84}.

Due to the insurmountable difficulties in making use of mathematical optimization fashions to acquire the precise answer of manufacturing scheduling, some researchers flip to approximate algorithms, comparable to genetic algorithms, random, native search, particle swarm algorithms, and simulations, to acquire a number of “excellent” plans^{85,86,87,88,89,90,91,92,93,94,95,96,97}.

Within the means of manufacturing schedule optimization, along with exploring mathematical strategies to resolve the issue, one other issue is to contemplate the precise influencing elements of the optimization course of. Within the examine of the standard optimization drawback, first, it’s assumed {that a} recognized issue might have an effect on the optimization of the manufacturing schedule. For instance, most research decide the mine manufacturing capability in line with the Taloy system, related mine elements, or related expertise after which optimize the mining sequence primarily based on the decided manufacturing capability. Lastly, the related infrastructure is allotted in line with the manufacturing scheduling^{98,99,100,101} set boundary grades in numerous intervals with the utmost internet current worth as the target operate to make sure that the infrastructure meets the utmost complete processing capability of mining, beatification and smelting. This technique can receive increased financial advantages than the Lane technique; nonetheless, the attribute of uniform grade distribution just isn’t relevant to most mines. On the aspect, the strategy described by Khan and Asad et al. focuses on the impression of geological uncertainty, advertising and marketing setting change and danger administration on manufacturing scheduling^{83,101,102,103,104,105,106,107,108}.

Consequently, because of the excessive complexity of manufacturing scheduling optimization and the issue of discovering an actual answer, it’s nonetheless a preferred analysis subject. Many issues within the means of manufacturing scheduling optimization of open pit mines exist, comparable to low operation effectivity brought on by great amount of calculation, disorderly enlargement of manufacturing capability brought on by the dimensions impact, and difficulties in concurrently optimizing the three components because of the interplay relationship. In view of those issues, taking the utmost complete internet current worth (NPV) as the target operate, the strategy of cellular capability search area is proposed to enhance the operation effectivity, the infrastructure funding operate primarily based on the utmost manufacturing capability is constructed to limit the manufacturing capability, the power idle threshold is designed to cut back the fluctuation vary of manufacturing capability, and the enumeration technique is used to judge all workable paths to understand the simultaneous optimization of the manufacturing capability, mining sequence and mining lifetime of open pit mines.

Mathematical mannequin of discrete physique dynamic programming

The aim of manufacturing scheduling optimization of open pit mines is to find out how a lot ore and rock are extracted and stripped yearly, the place they’re superior and the way lengthy the mining life is. Due to this fact, the deposit ought to be divided right into a finite variety of discrete our bodies, which ought to be taken as the choice objects of open pit mining on the finish of the yr. Because of the traits of open pit mining know-how and security necessities, mining engineering must be carried out progressively from high to backside in accordance with the desired slope angle, and the division of discrete our bodies wants to fulfill the geometric area relationship. In keeping with the definition and technology precept of the “geological optimum pit” proposed by¹, a sequence of absolutely nested discrete our bodies, specifically, the “geological optimum pit sequence”, will be obtained. The particular course of for producing the “geological optimum pit sequence” is as follows:

Began from the underside of the last word pit (additionally the primary geological optimum pit), floating cone exclusion technique is used to search out out all of the elements whose ore quantity is the same as the given increment (comparable to 2 million tons), and amongst these elements, the one which holding the bottom common grade faraway from the last word pit, leaving a pit that’s 2 million tons lower than the last word pit. The pit has the very best metallic content material of all of the pits, with 2 million tons much less ores than the last word pit. So the second geological optimum pit (the primary is the last word pit) is obtained. Then, within the remaining pit (the second geological optimum pit), take away the half with the ore quantity equal to the given increment (2 million tons) and the minimal common grade by the identical technique, and a smaller pit (the third geological optimum pit) is obtained. In keeping with the strategy analogy, the last word pit is discretized right into a sequence of utterly nested discrete physique sequences, that’s to say, the geological optimum pit sequence.

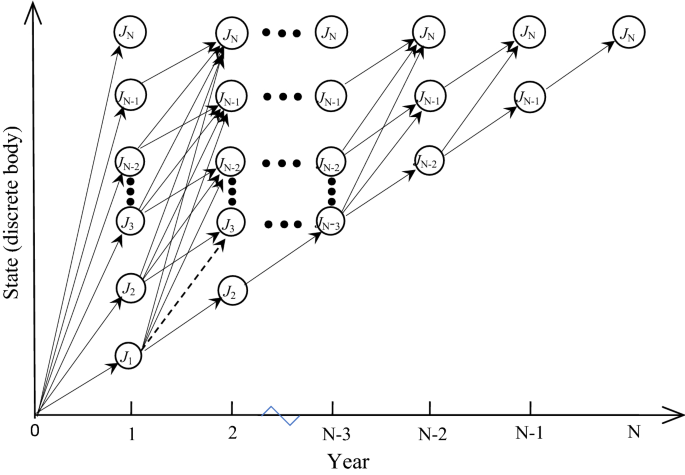
The discrete our bodies are put into the dynamic sorting mannequin as state variables, as proven in Fig. 1.

Discrete physique dynamic sorting.

The circles in Fig. 1 characterize a discrete physique (geological optimum pit), which can also be the place the pit is advancing on the finish of a yr. The 2 circles linked by arrows, comparable to J₁ within the first yr and J₃ within the second yr, linked by dotted arrows, point out that the open pit advances to J₁ within the first yr and J₃ within the second yr. In geometric area, J₃ utterly comprises J₁, subsequently the amount of ore equivalent to J₁ and J₃ will be expressed as O₁,₁ and O₂,₃, and the amount of rock will be expressed as R_1,1 and R_2,3. In reality, because the portions of ore and rock of every discrete physique have been decided, O_1,1 and O_2,3 are equal to O₁ and O₃; R_1,1 and R_2,3 are the identical as R₁ and R₃, primarily for the aim of referring to time. Then, the amount of ore and rock of the jth discrete physique equivalent to the ith yr will be expressed as O_i,j and R_i,j, respectively. Due to this fact, the amount of ore o_{i−1, ok} (i, m) and rock produced from discrete physique J_ok in yr i − 1 to discrete physique J_m in yr i the place m > ok, as a result of the discrete physique have to be superior from small to giant, are r_i−1,ok (i, m), respectively:

the place γ is the ore restoration charge and δ is the blending charge of waste rock.

The focus quantity v_i-1,_ok(i, m), which transitions from the discrete physique J_ok in yr i − 1 to the discrete physique J_m in yr i, is:

the place g_ok and g_m characterize the common grade of ore within the okth and mth discrete our bodies; g_r represents the common grade of rock (R_i-1,ok − R_i,m) transiting from discrete J_ok to discrete J_m; g_v refers to pay attention grade.

The revenue u_{i − 1},_ok(i, m), which transitions from the discrete physique J_ok in yr i − 1 to the discrete physique J_m in yr i, is:

the place p_v refers back to the worth of focus, ¥/t; c_o, c_p and c_r characterize mining value, processing value and stripping value, respectively, ¥/t; and η and ε characterize the worth rise charge and price rise charge, respectively.

The online current worth NPV_i-1,_ok (i, m), which transitions from the discrete physique J_ok in yr i − 1 to the discrete physique J_m in yr i, is:

the place λ represents the low cost charge.

The transition course of talked about above is the transition course of between completely different states. With out contemplating the constraints of manufacturing capability, any yr in Fig. 1 often is the closing lifetime of the mine. Additionally it is the yr during which the mine is mined to the ultimate state J_N (discrete physique, which can also be the last word pit of the open pit mine). Along with the three manufacturing prices of mining, stripping and processing given in Eq. (4), one other important value is infrastructure funding. It usually happens on the preliminary stage of mine development, i.e., the infrastructure funding doesn’t have an effect on the state transition proven in Fig. 1. Nonetheless, it’ll have an effect on the ultimate financial good thing about the mine. Due to this fact, it’s mandatory to contemplate the infrastructure funding in every NPV that reaches the ultimate state J_N by completely different paths. Though infrastructure funding has no affect on a state transition, infrastructure funding is affected by mine manufacturing capability, and mine infrastructure funding normally wants to fulfill the utmost manufacturing capability in the entire life cycle of the mine. In different phrases, the infrastructure funding wants to fulfill the utmost ore amount distinction between any two adjoining time factors within the state transition course of on a path to the ultimate state J_N, as proven in Fig. 1; that’s, the utmost manufacturing capability on this path is max{o_i-1,ok(i, m)}. In keeping with Eq. (1), the amount of ore produced by state transition at two adjoining time factors is o_i-1,_ok(i, m). Due to this fact for a selected path L(D) with a mining lifetime of D years, its most manufacturing capability q_L(D) is:

The infrastructure funding of the mine will be approximated as a linear operate of the utmost manufacturing capability of the ore. For the trail L(D) with a mining lifetime of D years, the infrastructure funding c_L(D) will be approximated as:

the place a refers back to the infrastructure funding base unrelated to the manufacturing scale, 10⁴ ¥, and b refers back to the infrastructure funding per unit of mining quantity, ¥/t.

The excellent financial profit NPV_L(D) for path L(D) will be expressed by the next system:

Enumeration optimization algorithm of manufacturing scheduling

Set a large sufficient vary of ore manufacturing capability [q_low, q_up], and the optimum manufacturing capability have to be inside this vary. This vary is about by the consumer and is the enter knowledge. Let n characterize the ordinal variety of the constraint area of ore manufacturing capability, and [q_Lⁿ, q_Uⁿ] outline the nth constraint area (capability search area).

• The 1st step: Set n = 1 and juxtapose the Bohr variable LastPlan = false. Within the discrete physique sequence {J}_N, the discrete physique whose ore amount is larger than or equal to and closest to q_low is discovered, and its quantity is denoted as H.

• Step two: Set the decrease bounds q_Lⁿ and higher bounds q_Uⁿ of the constraint area [q_Lⁿ, q_Uⁿ]:

  $$q_{{textual content{L}}}^{n} = {textual content{O}}_{{textual content{H}}} {-}Delta {textual content{P}}/{2}$$

  (9)

  the place ΔP is the ore increment of the pit set when the discrete physique sequence {J}_N is generated¹, and O_H is the ore amount of the Hth discrete physique within the sequence {J}_N.

  

  (10)

  the place O_N is the whole ore amount within the final pit and x₁, x₂, x₃ are the search area constraints, that are decided in line with the scale of the mine. If G > N obtained by Eq. (10), set G = N. The higher sure of the area is

  $$q_{{textual content{U}}}^{n} = {textual content{O}}_{{textual content{G}}} + Delta {textual content{P}}/{2}$$

  (11)

  the place O_G is the ore amount of the Gth discrete physique in sequence {J}_N.

  If q_Uⁿ > q_up, LastPlan = true.

• Step three: Discover all manufacturing scheduling whose annual ore output meets the constraints of the area [q_Lⁿ, q_Uⁿ]. That’s, discover all subsequences during which the annual ore output falls into the area [q_Lⁿ, q_Uⁿ]. Calculate the NPV of every schedule, report the schedule with the very best NPV, and name the schedule the “native greatest schedule” within the area [q_Lⁿ, q_Uⁿ]. The particular technique is as follows:

  • Step 1: Set i = 1 (first yr). A discrete physique is discovered within the discrete physique sequence {J}_N. The ore amount is at least and closest to q_Lⁿ, the decrease restrict of the constraint area [q_Lⁿ, q_Uⁿ] of the set ore manufacturing capability, and the whole amount of ore and rock is not more than q_up of the set annual mining and stripping capability. If such a discrete physique is discovered, its quantity in {J}_N is H(1); that’s, the pit on the finish of the primary yr on the deliberate path L underneath development is superior to pit J_H(1)*. In keeping with Eqs. (1), (3), calculate the portions of produced ore o₁, focus v₁ and stripped waste rock r₁ on this yr. Then, calculate the annual revenue u₁ and its internet current worth NPV₁ discounted to time 0 in line with Eqs. (4), (5). Transfer on to the following step. If such a discrete physique just isn’t discovered, there isn’t any workable schedule, and the algorithm terminates.

  • Step 2: set i = i + 1 (subsequent yr).

  • Step 3: The discrete physique quantity H(i) is the same as H(i − 1) + 1 in yr i, and H(i-1) is the discrete physique variety of the earlier yr of the deliberate path L underneath development.

  • Step 4: In keeping with Eqs. (1), (2), calculate the ore mining amount o_i and waste rock stripping amount r_i from i − 1 to i.

  • Step 5:

    1. (A)

       If o_i < q_Lⁿ and o_i + r_i ≤ q_up.

    2. (B)

       H(i) = N, that’s, the discrete physique J_H(i) is the final (final pit) within the sequence {J}_N, then the deliberate path L underneath development has reached the tip level, and the ultimate state J_N is the discrete physique of the tip level on the trail. A whole workable deliberate path is obtained, and its mining life D = i. In keeping with Eq. (3), the focus amount v_i within the first yr is calculated, after which in line with Eq. (4–5), the annual revenue u_i and its internet current worth NPV_i discounted to time 0 are calculated. Go to step 6.

    3. (C)

       H (i) < N, the ore amount of yr i is decrease than the decrease restrict of the set annual ore manufacturing capability, which isn’t workable. Set the discrete physique quantity H(i) to H(i) + 1, that’s, think about a bigger discrete physique, and return to step 4.

    4. (D)

       q_Lⁿ ≤ o_i≤ q_Uⁿand o_i + r_i ≤ q_up.

       Discrete physique J_H(i) is the workable pit state on the finish of i on the deliberate path L underneath development. In keeping with Eq. (3), the concentrated amount v_i of yr i was calculated. Then, in line with Eqs. (4), (5), the annual revenue u_i and its internet current worth NPV_idiscounted to time 0 had been calculated. If H(i) = N, then the deliberate path underneath development has reached the ultimate state, and an entire workable deliberate path has been obtained. Set the mining lifetime of the meant path to D = i and perform step 6. In any other case, return to step 2.

    5. (E)

       If o_i > q_Uⁿ or o_i + r_i > q_up.

       The
       amount of ore mining or the whole amount of mining and stripping in yr i exceeds the set higher restrict, there isn’t any workable plan, and the algorithm terminates.

  • Step 6: So far, a workable deliberate path with “minimal ore output” is obtained, that’s, the amount of ore extracted in every year of the trail besides the final yr is simply sufficient to fulfill the set minimal annual ore manufacturing capability q_Lⁿ. Calculate the infrastructure funding c _L(D) of the shcedule in line with Eqs. (6), (7). Calculate the whole NPV _L(D) of this path in line with Eq. (8). Take the trail as the present path and put it aside as the most effective path.

  • Step 7: Set time i = D − 1, the place D is the mining life of the present path L.

  • Step 8: Construct a brand new workable plan path ranging from yr i. The brand new path would be the identical as the present path in yr 1 to (i − 1). Add 1 to the present path’s discrete physique variety of yr i, that’s, set H(i) = H(i) + 1.

  • Step 9: In keeping with Eqs. (1), (2), calculate the ore amount o_i and waste rock amount r_i from i − 1 to i.

  • Step 10: Distinguish feasibility and financial analysis, divided into two circumstances:

    1. (A)

       If o_i< q_Uⁿ and o_i + r_i ≤ q_up.

       Discrete physique J_H(i) is the workable pit state on the finish of yr i of the brand new deliberate path being constructed, and it turns into the discrete physique of final yr i of the present path (that’s, the unique discrete physique is changed). In keeping with Eq. (3), the concentrated amount v_i of yr i is calculated. Then, in line with Eqs. (4), (5), the annual revenue u_i and its internet current worth NPV_idiscounted to time 0 are calculated. If H(i) = N, the brand new deliberate path underneath development has reached the ultimate state and an entire workable deliberate path has been obtained, and its mining life is D = I; go to step 15. In any other case, go to step 11.

    2. (B)

       If o_i > q_Uⁿ or o_i + r_i > q_up.

       If the amount of ore mining or the whole amount of mining and stripping in yr i exceeds the higher restrict set, it isn’t workable. Set i = i − 1, that’s, return one yr alongside the present path. If i > 0, return to step 8. In any other case, all workable plan paths are constructed and evaluated; proceed to step 16.

  • Step 11: Set i = i = i + 1.

  • Step 12: The discrete physique quantity H(i) is the same as H(i − 1) + 1 in yr i, the place H(i-1) is the discrete physique variety of the earlier yr of the brand new deliberate path being constructed.

  • Step 13: In keeping with Eqs. (1), (2), calculate the ore amount o_i and waste rock stripping amount r_i from i − 1 to i.

  • Step 14:

    1. (A)

       if o_i< q_Lⁿ and o_i + r_i ≤ q_up, in two circumstances:

    2. (B)

       H(i) = N, that’s, the discrete physique J_H(i) is the final (final pit) within the sequence {J}_N, the brand new deliberate path underneath development has reached its endpoint, and the last word pit J_N is the tip discrete physique on this path. Lastly, an entire workable deliberate path is obtained, and its mining life D = i. In keeping with Eq. (3), the concentrated amount v_i of yr i was calculated, after which in line with Eqs. (4), (5), the annual revenue u_i and its internet current worth NPV_i discounted to time 0 had been calculated. Carry out step 15.

    3. (C)

       H(i) < N, the ore amount of yr i is beneath the decrease restrict of the set ore manufacturing capability, which isn’t workable. Set discrete physique quantity H(i) = H(i) + 1, that’s, think about a bigger mining discrete physique, and return to step 13.

       If q_Lⁿ ≤ o_i≤ q_Uⁿ and o_i + r_i ≤ q_{up x}.

       Discrete physique J_H(i) is the workable state on the finish of yr i on the brand new plan path underneath development. In keeping with Eq. (3), the concentrated
       amount vi of yr i was calculated, after which in line with Eqs. (4), (5), the annual revenue u_i and its internet current worth NPV_i discounted to time 0 had been calculated. If H(i) = N, then the brand new deliberate path underneath development has reached the ultimate state, and an entire workable deliberate path has been obtained. Its mining life is D = i, and step 15 is carried out. In any other case, return to step 11.

    4. (D)

       If o_i > q_Uⁿ or o_i + r_i > q_up.

       The amount of ore mining or the whole amount of mining and stripping in yr i exceed the set higher restrict, which isn’t workable. The algorithm offers up midway and shows error data. Go to step 16 and output the most effective path so far.

  • Step 15: After a brand new workable scheduling path is established, calculate the infrastructure funding c_L(D) of the schedule in line with Eqs. (6), (7). Calculate the whole NPV _L(D) of this path in line with Eq. (8). If the whole NPV _L(D) of this path is larger than the whole NPV _L(D) of the saved greatest path, the trail is reserved as the most effective path (that’s, the unique greatest path is changed); in any other case, the unique optimum path stays unchanged. Take this path as the present path and return to step 7.

  • Step 16: Output the best-planned path on the interval [q_Lⁿ, q_Uⁿ].

• Step 4: If LastPlan = false, go to the following step. In any other case, if LastPlan = true, go to step six.

• Step 5: Set n = n + 1 and H = H + 1. Return to step two and set the following constraint area, and proceed the iteration. On this iteration course of, each time H will increase by 1, the decrease sure q_Lⁿ of the area calculated in line with Eq. (9) will increase as soon as. The entire area additionally strikes to the next manufacturing capability.

• Step six: The constraint area covers your complete vary of ore manufacturing capability [q_low, q_up]. The most effective schedule is obtained by discovering the one with the very best NPV amongst all of the native greatest schedules recorded; Output the most effective schedule. The algorithm also can output all native greatest schedules to see how NPV varies with ore manufacturing capability. The algorithm ends.

Within the above algorithm, the bigger the width of the constraint area (q_Lⁿ, q_Uⁿ) is, the extra schedules fulfill the constraint of (q_Lⁿ, q_Uⁿ). If the area is about broad, the variety of schedules to be evaluated in step three is simply too giant and time-consuming. If the vary is simply too slim, the chance of lacking the optimum schedule is excessive. The situations listed in Eq. (10) in step two are to regulate the width of the constraint area inside such a spread. As well as, for a given area width, the variety of schedules s satisfying the area constraint will increase quickly with rising mining life. The detailed algorithm movement is proven in Fig. 2.

Movement chart of enumeration optimization algorithm for manufacturing scheduling.

Among the many workable scheduled paths, the distinction between some paths’ complete NPV and most complete NPV may be very small, which will be ignored. Nonetheless, some paths could also be extra cheap than these with the utmost complete NPV, comparable to extra steady ore yield and decrease peel peak. Due to this fact, within the above algorithm, a number of optimum paths will be reserved and output for customers to decide on. When designing optimization software program, the variety of optimum paths to be reserved ought to be set by customers as enter knowledge on the interface.