Quantum-behaved particle swarm optimization primarily based on solitons

[ad_1]

Particle swarm optimization (PSO)

Particle swarm optimization belongs to a department of the SI algorithm that was first meant for simulating social habits after which developed for constrained and unconstrained issues and in addition utilized in discrete and steady optimization issues. It was first developed by Kennedy and Eberhart in 1995⁴. The principle thought of the PSO algorithm is to share the perfect place of the entire swarm in each era after which transfer them towards their very own best-known place and your entire swarm’s best-known place within the search area concurrently. Then, particles are up to date in accordance with the next equation:

$$start{aligned} V_{i,j}(t+1)= & {} wV_{i,j}(t)+c_{1} r_{1} left( p_{Best_{i,j}}- X_{i,j}(t) proper) + c_{2} r_{2} (g_{Best_{j}} – X_{i,j}(t)), X_{i,j}(t+1)= & {} X_{i,j}(t)+V_{i,j}(t+1),~qquad i=1,2, ldots , M,qquad j=1,2,ldots , D, finish{aligned}$$

the place (x_{ij}(t)) and (v_{ij}(t)) are the worth and velocity of (j{textual content {th}}) variable of the (i{textual content {th}}) particle throughout the (t{textual content {th}}) iteration, respectively. M is the dimensions of the inhabitants, D is the dimension, (p_{Best_{i,j}}) is the (j{textual content {th}}) variable of the (i{textual content {th}}) greatest answer up to now, (g_{Best_j}) is the (j{textual content {th}}) variable of the worldwide greatest particle within the swarm, (c_1), and (c_2) are “Private Studying Coefficient” and “International Studying Coefficient”, respectively, that are predefined, w is a continuing, often called “Inertia Weight”, and management the worldwide and native search potential of PSO and (r_1) and (r_2) are random numbers in [0, 1]. This course of iterates in order to achieve the suitable health or attain most iterations.

The pseudo-code of the PSO algorithm is illustrated in Algorithm 1.

JAYA algorithm

The JAYA algorithm is a meta-heuristic algorithm lately developed for constrained and unconstrained issues and can also be utilized in discrete and steady optimization issues. It was first developed by Rao in 2016²³. On this algorithm, two parameters must be initialized for any optimization issues: the dimensions of the inhabitants, and the utmost variety of iterations. Then preliminary options are randomly generated within the possible area. Afterward, the health value of the generated options is calculated and the perfect and the worst options within the inhabitants are recognized. Then every variable of each answer is up to date in accordance with the next equation:

$$start{aligned} X_{i,j}(t+1) = X_{i,j}(t) + r_{1} left( X_{j,greatest}- vert X_{i,j}(t) vert proper) -r_{2} left( X_{j,worst}- vert X_{i,j}(t) vert proper) , finish{aligned}$$

(1)

the place (X_{i,j}(t)) is the worth of the (j{textual content {th}}) variable for the (i{textual content {th}}) candidate throughout the (t{textual content {th}}) iteration, (X_{j,greatest}) is the worth of the variable j for the perfect candidate and (X_{j,worst}) is the worth of the variable j for the worst candidate. (X_{i,j}(t+1)) is the up to date worth of (X_{i,j}(t)) and (r_{1}) and (r_{2}) are random numbers in (left[ 0,1right]). If the brand new answer is in a greater situation than the present one, it’s changed by the brand new one. This process is repeated in order to attain the suitable health or attain most iterations.

Improved sine cosine algorithm

Sine cosine Algorithm (SCA) is a physics-based algorithm and was first developed by Mirjalili et al. in 2016 for fixing optimization issues⁷. The principle disadvantage of SCA is having low optimization precision and native minima trapping because of its exploration and exploitation mechanism. In Ref.²⁴ the authors proposed a novel technique to beat the weak spot of the algorithm by substituting a brand new replace mechanism. They proposed a brand new model of SCA referred to as Improved Sine Cosine algorithm (ISCA). Much like different meta-heuristic optimization ISCA begins the optimization course of by producing the preliminary options randomly within the possible area. Afterward, the health value of the generated options is calculated and the perfect answer within the inhabitants is recognized. Then every variable of each answer is up to date in accordance with the sine and cosine capabilities as follows:

$$start{aligned} X_{i,j}(t+1)=left{ start{array}{rl} X_{i,j}(t) + r_{1}(t) sin (r_{2}) displaystyle Huge vert r_{3} P_{i,j}(t)- X_{i,j}(t)Huge vert &{} if quad r_{4} geqslant 0.5, X_{i,j}(t) + r_{1}(t) cos (r_{2}) displaystyle Huge vert r_{3} P_{i,j}(t)- X_{i,j}(t)Huge vert &{} if quad r_{4} < 0.5, finish{array} proper. finish{aligned}$$

the place (X_{i,j}(t)) is the worth of the (j{textual content {th}}) variable for the (i{textual content {th}}) candidate throughout the (t{textual content {th}}) iteration, (P_{j}(t)) is the (j{textual content {th}}) variable of the perfect answer throughout the (t{textual content {th}}) iteration. (X_{i,j}(t+1)) is the up to date worth of (X_{i,j}(t)) and (r_{1}(t)) is described as follows:

$$start{aligned}r_{1}(t)=a left( 1- left( frac{t}{T} proper) ^alpha proper) ^beta ,finish{aligned}$$

during which (alpha) and (beta), are constructive actual numbers. (r_{2}), (r_{3}), and (r_{4}) are random numbers within the vary (left[ 0,1right]). If the brand new answer is in a greater situation than the present one is changed by the brand new one. This process is repeated in order to attain the suitable health or attain most iterations.

Quantum particle swarm optimization (QPSO)

Nature is actually primarily based on quantum mechanical guidelines, though the quantum results are extra vital in micro-scale programs. One of many elementary ideas of quantum mechanics is wave-particle duality, during which all of the details about a particle (state of affairs, place, velocity, power, and so forth.) is described as a wave operate, (psi (r,t)), comparable to a normalized quantum eigenstate. From the quantum viewpoint, a wave packet, which is a superposition of too many waves, can symbolize a localized particle in area underneath a bodily potential, however it’s broadened to some extent because of the uncertainty precept. In accordance with the Heisenberg uncertainty precept, the precise place of a quantum particle and its velocity can’t be concurrently decided. That’s true for its power and its quantum state lifetime as effectively. Subsequently, the expectation worth of every amount in quantum mechanics is represented as a probabilistic worth, which is decided by the chance density operate, (|psi (r,t)|^2), which describes the chance of a particle to be present in a given quantum state (a given place, momentum, power, and so forth). Within the final years, many researchers have tried to introduce quantum ideas by numerous mathematical frameworks and succeeded in using them in optimization algorithms. The quantum particle swarm optimization (QPSO) algorithm is impressed by the quantum habits of nature. The principle thought behind the QPSO is to discover a correct wave operate, related to a quantum particle in a possible subject. To search out the optimum answer, QPSO exploits the quantum chance density operate to guide particles to the most probably positions (or to essentially the most attainable states in a extra normal sense). Because of the probabilistic nature of quantum mechanics, the correlation between quantum particles, and the mutual affect of their eigenstates, it’s anticipated that the answer lies in essentially the most possible area of the search extent. Though there may be not an specific relation between quantum options and the time complexity, it’s anticipated that the answer lies in essentially the most possible area of the search extent, leading to higher looking out efficiency. The QPSO algorithm, primarily based on some quantum potential fields, corresponding to sq. effectively, 1D potential effectively, the 1D-quantum easy harmonic oscillator, Coulomb-like sq. root subject, Lorentz potential subject, and Rosen–Morse has been already used and developed by a number of authors^14,21,22. The quantum wave capabilities utilized in the entire talked about research fulfill the standard linear Schrödinger equation,

$$start{aligned} ihbar frac{partial psi }{partial t}+frac{hbar ^2}{2m}frac{partial ^2psi }{partial x^2}-V(x,t)psi =0. finish{aligned}$$

(2)

Then again, there are a lot of pure phenomena in physics and engineering, described by nonlinear equations. The Korteweg–de Vries equation, the nonlinear Schrödinger equation, the coupled nonlinear Schrödinger (NLS) equation, and the sine-Gordon equation are some well-known nonlinear equations which have been used extensively in reference to many bodily phenomena. They’re precisely solvable equations with soliton-like options.

Within the sequel, we current the chance density operate of such issues, particularly, quantum solitons with a self-consistent answer to the NLS equation.

Solitons

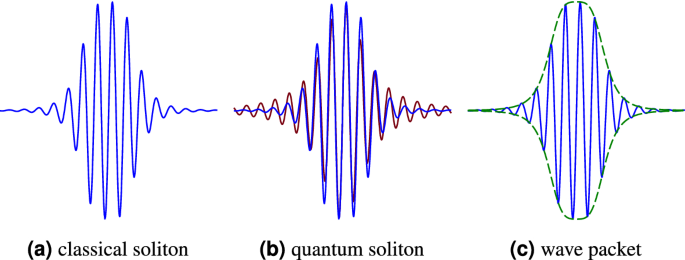
Solitons or solitary waves are basically the analytical options of bodily integrable nonlinear partial differential equations. They’re ubiquitous phenomena each in classical and quantum points with an unlimited variety of functions Classical solitons in physics are non-dispersive pulses, touring lengthy distances (Fig. 1a). One of the vital fascinating and distinctive options of solitons is having neither deformation nor attenuation throughout propagation in a nonlinear dispersive medium. Making the most of the nonlinearity of the medium, solitons can reconstruct themselves, regardless of dispersion results. Quantum solitons are certainly the quantum states of classical options (Fig. 1b). They’re handled as particle-like wave packets with their very own coherent eigenstates and power eigenvalues (Fig. 1c).
The quantum solitons are one of the vital frequent options of the quantum NLS equation which governs many quantum phenomena in physics and engineering. The same old Schrödinger equation, (Eq. (2)), turns into nonlinear if the potential V(x, t) will depend on (psi), itself. The final normal dimensionless type of the NLS equation so reads,

$$start{aligned} i frac{partial psi }{partial t}+pfrac{partial ^2psi }{partial x^2}+q|psi |^2psi =0, finish{aligned}$$

(3)

during which (i=sqrt{-1}), and p and q are the coefficients with a particular bodily significance. Its primary soliton-like answer is,

$$start{aligned} psi (x,t)=frac{1}{2}sqrt{frac{2A}{q}}frac{exp (iAt)}{cosh (frac{A}{2p}x)}, finish{aligned}$$

(4)

the place A is an arbitrary fixed associated to the wave packet’s properties (amplitude, width, and frequency). A extra normal model of the NLS equation is written by way of the Hamiltonian operator ({hat{H}}), as follows:

$$start{aligned} i frac{partial psi }{partial t}={hat{H}}psi + Vpsi +q|psi |^2psi . finish{aligned}$$

(5)

On this equation, ({hat{H}}) corresponds to the associated kinetic and potential energies of the system, and is a quadratic operate of the momentum operator, ({hat{p}}=-ipartial /partial x) and ({hat{x}}), specifically, It has a normal soliton-like answer as the next type,

$$start{aligned} psi (x,t)=textsf {A}(x,t)F(z)e^{iS(x,t)}, finish{aligned}$$

(6)

which describes a touring soliton with the profile operate F(z) by way of a wave-type argument z²⁵. The quantum NLS in its normal type normally is written as,

$$start{aligned} ihbar frac{partial psi }{partial t}=-frac{hbar ^2}{2m}frac{partial ^2psi }{partial x^2}+2c|psi |^2psi , finish{aligned}$$

(7)

the place, c, because the coupling parameter is an actual quantity. It’s constructive within the repulsive NLS and unfavourable within the engaging NLS, which arises from the Hamiltonian,

$$start{aligned} {hat{H}}=int ({psi _x}psi _x+cpsi ^{*}psi ^{*}psi psi )dx. finish{aligned}$$

(8)

The quantum solitons are the options of the engaging NLSs. Taking a fast have a look at the answer of some issues, one can discover the stationary quantum solitons to be as the next normal dimensionless type,

$$start{aligned} psi = alpha frac{e^{iS}}{cosh (beta x)}, finish{aligned}$$

(9)

during which, (1/beta) denotes the attribute size outlined in the issue. It’s value noting that the wave operate, (psi), must be normalized in area, specifically,

$$start{aligned} int _{-infty }^{+infty }|psi |^2dx=1. finish{aligned}$$

(10)

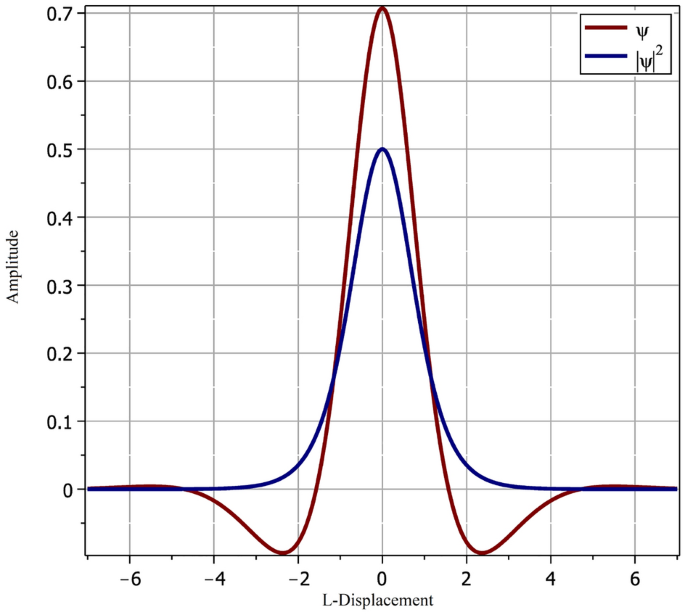
The corresponding chance density operate, (|psi |^2), is given by,

$$start{aligned} |psi |^2=frac{alpha ^2}{cosh ^2(beta x)}, finish{aligned}$$

(11)

plotted in Fig. 2.

As one can see in Supplementary Appendix, though the wave capabilities could be different in accordance with the given potential, its normal type stays unchanged.

Within the subsequent half, we intend to make use of the final soliton-solutions of the NLS equation within the QPSO.

Quantum soliton-inspired optimization algorithms

The principle technique right here is precisely the identical because the QPSO situation proposed by many authors^14,19,21,22, however with an M variety of particle-like quantum soliton wave packets as an alternative of quantum particles.

In Ref.²⁶ the authors have proven that, geometrically, the perfect place of the particle most probably is positioned on the linear convex mixture of the perfect native and world place often called native attractor (K_{i}(t)= left( K_{i,1}(t), K_{i,2}(t), ldots , K_{i,D}(t) proper)) outlined as follows

$$start{aligned} K_{i,j}(t)= & {} lambda ~ p_{Best_{i,j}}(t) + left( 1- lambda proper) g_{Best_{j}}(t), quad i=1,2,ldots ,M, quad j=1,2,ldots ,D, nonumber lambda= & {} frac{c_{1}r_{1}}{c_{1}r_{1}+c_{2}r_{2}}. finish{aligned}$$

(12)

In accordance with this trajectory evaluation, we’ve a brand new motion technique relating to the perfect native, (p_{Best_i}(t)), and world place of the entire swarm, (g_{Greatest}(t)). The brand new place on this mannequin could be up to date as follows^14,26,

$$start{aligned} x_{i}(t+1)= K_{i}(t)+L ( X_{i}(t), u), finish{aligned}$$

(13)

the place L denotes a displacement operate relying on the attribute size of the issue and a non-uniform distribution operate, F.

$$start{aligned} L=frac{1}{beta } F. finish{aligned}$$

(14)

The attribute size, representing a bodily significance, outlined as absolutely the distinction of common place of all particles’ private greatest positions in swarm and the present place, that’s

$$start{aligned} frac{1}{beta }= Huge vert X_{i}(t)-frac{1}{M}sum _{i=1}^{M} p_{Best_{i}}(t)Huge vert . finish{aligned}$$

(15)

The distribution operate, F, which is implicitly associated to the chance density operate, proposes the most probably place across the native attractor level and is decided as (G^{-1}(u)), during which u is a random quantity in [0, 1], and G as a random quantity generator simulated by the chance density operate, is assigned to u,

$$start{aligned} displaystyle G(L)=frac{vert psi (L) vert ^{2} }{max (vert psi (L) vert ^{2})}:=u. finish{aligned}$$

(16)

By substituting the chance density operate of quantum solitons, (displaystyle |psi |^2=alpha ^2/cosh ^2(beta L)), and fixing for L, we’ve

$$start{aligned}L=pm frac{1}{beta }cosh ^{-1}bigg (frac{1}{sqrt{u}}bigg ).finish{aligned}$$

Lastly, substituting L into Eq. (14), F(u) is derived as follows,

$$start{aligned} F(u)=pm cosh ^{-1}bigg (frac{1}{sqrt{u}}bigg ). finish{aligned}$$

(17)

Now, by substituting L in Eq. (13), the brand new place could be measured by making use of both of the next two equations:

$$start{aligned} X(t+1)= Ok(t) + frac{1}{beta }cosh ^{-1}bigg (frac{1}{sqrt{u}}bigg ), finish{aligned}$$

(a)

$$start{aligned} X(t+1)= Ok(t) – frac{1}{beta }cosh ^{-1}bigg (frac{1}{sqrt{u}}bigg ). finish{aligned}$$

(b)

In accordance with the quantum mechanical ideas, the quantum state (place) is undetermined till a measurement takes place. So (X(t+1)) could be up to date both by (a) or (b). Within the absence of statement, it’s certainly a superposition of each. In computation, the random operate has the identical function as that of the observer in experiments. To take action, let

$$start{aligned} X(t+1)=left{ start{array}{rl} (a) &{} if quad 0.5 leqslant upsilon leqslant 1, (b) &{} if quad 0 leqslant upsilon < 0.5, finish{array} proper. finish{aligned}$$

the place (displaystyle upsilon =rand[0,1]), then, the search radius decreases linearly by multiplying with an element w outlined as follows,

$$start{aligned} displaystyle w = w_{1} + frac{ (w_{0} – w_{1}) ,occasions, left( MaxIt – t proper) }{ MaxIt}, finish{aligned}$$

(18)

the place (w_0) and (w_1) are the preliminary and last values of w respectively. MaxIt is the utmost variety of iterations and t is the present search iteration quantity. Subsequently, Eq. (13) can rewritten as follows,

$$start{aligned} X_{i}(t+1)=left{ start{array}{rl} K_{i}(t) + w displaystyle Huge vert frac{1}{M}sum _{i=1}^{M} p_{Best_{i}}(t)- X_{i}(t)Huge vert cosh ^{-1}left( frac{1}{sqrt{u}}proper) &{} if quad upsilon geqslant 0.5 K_{i}(t) – w displaystyle Huge vert frac{1}{M} sum _{i=1}^{M} p_{Best_{i}}(t)- X_{i}(t)Huge vert cosh ^{-1}left( frac{1}{sqrt{u}}proper) &{} if quad upsilon <0.5 finish{array}. proper. finish{aligned}$$

The pseudo-code of the quantum soliton-inspired particle swarm optimization (QSPSO) algorithm is illustrated in Algorithm 2.