Optimization of tamoxifen solubility in carbon dioxide supercritical fluid and investigating different molecular targets utilizing superior synthetic intelligence fashions
[ad_1]
Determination tree
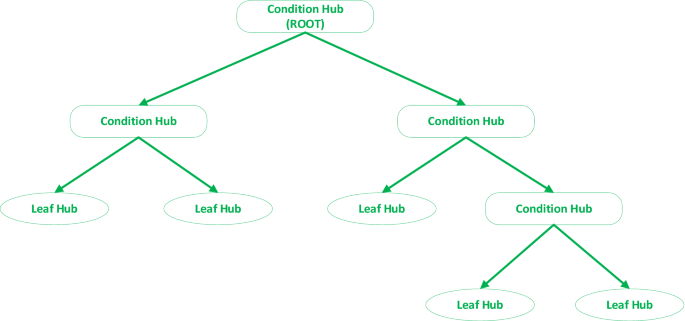
Timber are the numerous knowledge buildings in varied fields of synthetic intelligence. A choice tree (DT) is a process generally used to analyses knowledge. A choice tree might deal with both regression or classification duties. A typical determination tree is made up of determination nodes (make a question on an enter options), edges (results of a question and cross to the kid node), and terminal or leaf nodes (generate the output)25,26,27, as proven in Fig. 1.
Every function of a dataset is dealt with as a node or hub within the DT, by way of the foundation node to be unmatched. This strategy might be extra developed until a leaf node is recognized. The choice tree’s output could be the terminal node19,28,29. A few of the well-known determination tree induction algorithms comparable to CART19, CHAID25, C4.5, and C5.027,30.
AdaBoost
Freund and Schapire invented the AdaBoost31 to resolve the binary classification drawback. In AdaBoost technique, the basic idea is to create a number of weak predictors sequentially utilizing the coaching knowledge subset after which merge them utilizing a given method. First, an equal-weighted coaching knowledge is used to construct the weak predictor. Nonetheless, the weights of the examples within the coaching subset that had been incorrectly estimated are raised. The brand new weighted coaching knowledge is then used to construct the weak predictor for the following spherical. After repeating the above method, a number of weak predictors are obtained, and every predictor is assigned a rating based mostly on the associated classification error. Utilizing some rule to mix all weak predictors will end in a remaining sturdy predictor. A number of AdaBoost variants have been applied, every with its benefits and functions31,32,33.
Every xi occasion’s weight wi is about proportionally to the potential of being precisely estimated, and implicitly proportionally to the predictor Tt error t. Moreover, every predictor determination on a brand new instance’s remaining prediction is weighted in keeping with its efficiency throughout the studying22,34,35.
Following steps usually reveals AdaBoost workflow:
This strategy has a number of benefits, essentially the most distinguished of which is easier to make use of and requires fewer hyper-parameters to be tuned. AdaBoost shouldn’t be vulnerable to overfitting due to its design and methodology35.
Nu-SVR
A set of enter and output parameters provided as fundamental configuration {(x1, y1), …, (xn, yn)}. The purpose of the Nu-SVR technique is to compute the correlation indicated within the following Equation, as f(x) should in neighborhood of worth of y as attainable. It also needs to be as flat as possible. Since we wish to keep away from over-fitted fashions on this investigation36,37,38.
$${fleft( x proper) = wT;Phi left( x proper) + b}$$
(1)
On this equation, Φ(x) is asserted because the non-linear perform mapping the enter area to area of upper dimensions and b denotes the bias. wT can also be stands for the load vector. Optimization is the first goal of the duty: Closeness and flatness are two of the basic goals of this problem, which is why the principle purpose is to optimize37,38,39,40,41:
$$frac{1}{2}left| {leftlceil w rightrceil } proper| + {textual content{C}}left{ {Y cdotupvarepsilon + frac{1}{n}mathop sum limits_{i = 1}^{n} left( {xi + xi^{*} } proper)} proper}$$
(2)
In line with the circumstances:
$${textual content{y}}_{{textual content{i}}} – leftlangle {w^{T} cdot Phi left( x proper)} rightrangle – b leupvarepsilon + xi_{i}^{*} ,$$
(3)
$$leftlangle {w^{T} cdot Phi left( x proper)} rightrangle + b – y_{i} leupvarepsilon + xi_{i} ,$$
(4)
$$xi_{i}^{*} ,xi_{i} ge 0$$
(5)
right here ɛ is a distance between the f(x) and its precise quantity. Additionally, ξ, ξi are additional slack variables depicted in42, declares that distance of worth ξ above ɛ error are affordable. The parameter C, outline because the regularization quantity, signifies an equilibrium on the tolerance of error ɛ and flatness of f 38.
So, Y (0 < Y < 1) reveals the higher certain for the perform of margin errors in coaching quantities and defines the decrease certain for the fraction of assist vectors. Moreover, to handle the primary problem, the twin assertion has been created by way of establishing the Lagrange perform38:
$$start{aligned} & {textual content{L}}:frac{1}{2}left| {leftlceil w rightrceil } proper|^{2} + {textual content{C}}left{ {Y cdotupvarepsilon + frac{1}{n}mathop sum limits_{i = 1}^{n} left( {xi + xi^{*} } proper)} proper} – frac{1}{n}mathop sum limits_{i = 1}^{n} left( {eta xi + eta^{*} xi^{*} } proper) & quad – ;frac{1}{n}mathop sum limits_{i = 1}^{n} left( {upvarepsilon + xi_{i} + y_{i – } w^{T} cdot Phi left( x proper) – b} proper) – frac{1}{n}mathop sum limits_{i = 1}^{n} left( {upvarepsilon + xi_{i} + y_{i} + w^{T} cdot Phi left( x proper) + b} proper) – betaupvarepsilon finish{aligned}$$
(6)
a, a*, η, η*, β display the Lagrange multipliers, then a(*) = a·a*, by way of maximize Lagrange perform W = (sumnolimits_{i = 1}^{n} {left( {a_{i} – a_{i}^{*} } proper) cdot Phi left( x proper)}) and results in an issue with twin optimization38:
$${textual content{Maximizes}} – frac{1}{2}mathop sum limits_{i = 1}^{n} left( {a_{i} – a_{i}^{*} } proper) cdot left( {a_{j} a_{j}^{*} } proper) cdot kleft( {x_{i} x_{j} } proper) + mathop sum limits_{i = 1}^{n} y_{i} left( {a_{i} – a_{i}^{*} } proper);$$
(7)
Topic to:
$$mathop sum limits_{i = 1}^{n} left( {a_{i} – a_{i}^{*} } proper) = 0 left( 8 proper)$$
(8)
$$mathop sum limits_{i = 1}^{n} left( {a_{i} – a_{i}^{*} } proper) le CY$$
(9)
$$a_{i} ,a_{i}^{*} epsilon left[ {0,frac{C}{n}} right].$$
(10)
Since Ok(xi,xj) stands for the kernel perform outlined by way of Ok(xi,xj) = Φ(xi)T·Φ(xj). The answer to latest System yields to the Lagrange multipliers a, a*. An estimate of the perform (L) is obtained when weight W is swapped into latest equations:
$$fleft( x proper) = mathop sum limits_{n = 1}^{n} left( {a_{i} – a_{i}^{*} } proper) cdot ok(x_{i} ,x) + b$$
(11)
Tamoxifen targets beside estrogen receptors
Pubchem website was used for smiles retrieval of tamoxifen (https://pubchem.ncbi.nlm.nih.gov/compound/Tamoxifen#part=InChI). Smiles code obtained was as the next (CCC(=C(C1=CC=CC=C1)C2=CC=C(C=C2)OCCN(C)C)C3=CC=CC=C3), this code was fed into LigTMap internet server (https://cbbio.on-line/LigTMap/) to seek for different molecular targets of tamoxifen, chosen goal lessons on this search are Anticogulant, Beta_secretase, Bromodomain, Carbonic_Anhydrase, Hydrolase, Isomerase, Kinase,Ligase, Peroxisome, Transferase, Diabetes, HCV, Hpyroli, HIV, Influenza and Tuberculosis. Additionally, this smile code was inserted in swissADME internet server (http://www.swissadme.ch/index.php) to analyze its boiled egg mannequin along with the physicochemical parameters.
[ad_2]
Source_link