A hybrid grasping political optimizer with fireworks algorithm for numerical and engineering optimization issues

[ad_1]

Political optimizer and firework algorithm are novel algorithms with glorious efficiency proposed lately, that are impressed by completely different social pure phenomena and may successfully resolve optimization issues. The hybrid algorithm proposed on this paper takes the political optimization algorithm as the start line, and the explosion spark and Gaussian mutation spark mechanism of the firework algorithm are added to the search strategy of the political optimization algorithm to reinforce the efficiency of the algorithm. This part will briefly introduce these two algorithms.

Political optimizer

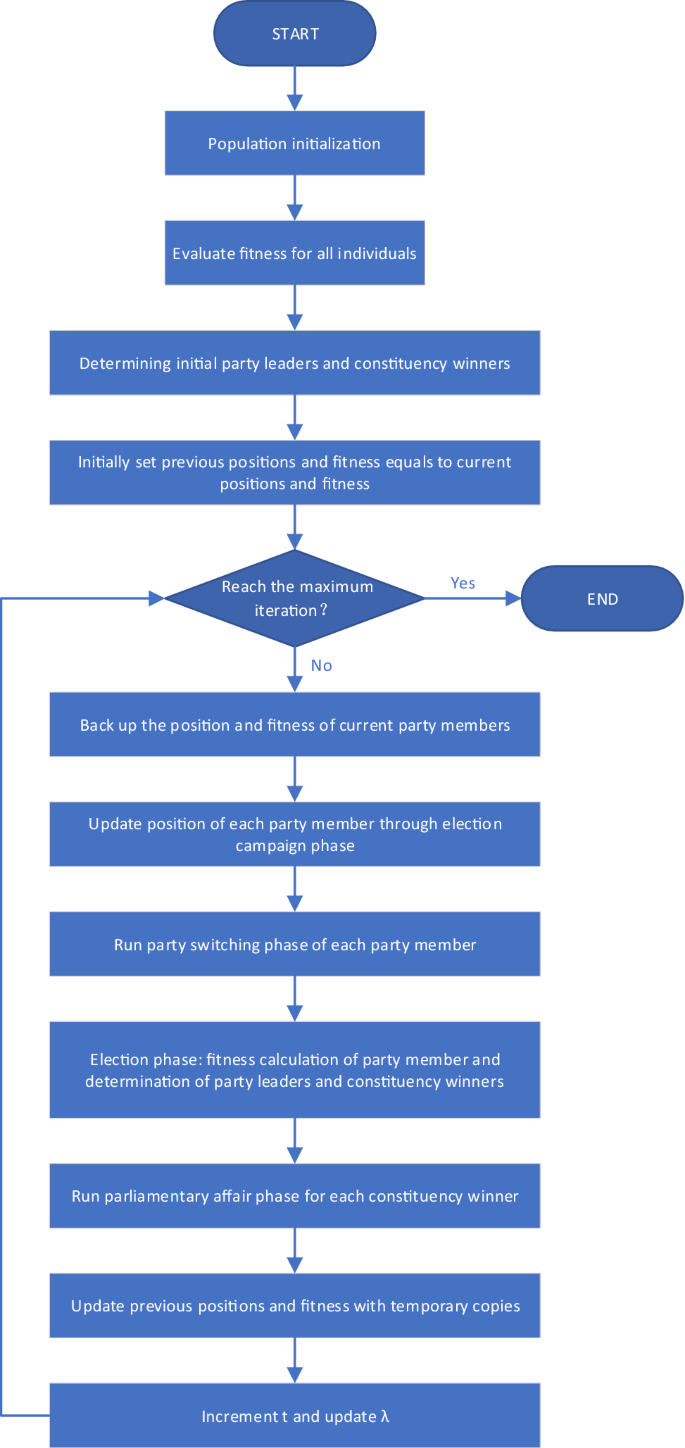
The political optimizer (PO) is a novel clever optimization algorithm impressed by the political election strategy of human society. In PO, every occasion member will be seen as a candidate resolution, and the election habits of occasion members will be seen as an analysis perform. As well as, the votes obtained by occasion members are mapped to the health worth of the candidate resolution. Not like conventional algorithms based mostly on political elections, PO considers the entire strategy of political elections, together with 5 phases of occasion formation and constituency allocation, election marketing campaign, occasion switching, inter-party election, and parliamentary affairs. PO seeks the optimum resolution by means of a multi-stage iterative course of, and its essential algorithm circulation is proven in Fig. 1. The next will introduce the 5 essential phases of PO.

Get together formation and constituency allocation

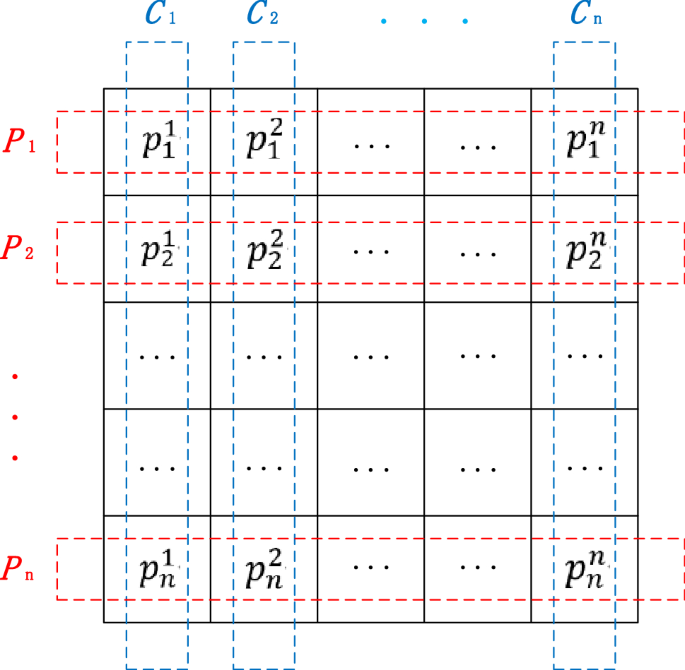
At the start of PO, all the inhabitants containing ({n}^{2}) people are divided into n events, and there are n members (candidate resolution) in every occasion. As well as, every occasion member additionally performs the function of an election candidate, that’s, one member from every occasion is chosen to kind a constituency. As is depicted in Fig. 2, the crimson dotted line signifies the division of political events, and the blue dotted line signifies the division of constituencies. The mapping of this inhabitants division to the mathematical mannequin is that all the inhabitants is split into n political events as proven in Eq. (1), and every occasion consists of n occasion members as represented as Eq. (2).

$$P = left{ {P_{1} ,P_{2} ,P_{3} , ldots ,P_{n} } proper}$$

(1)

$$P_{i} = left{ {p_{i}^{1} ,p_{i}^{2} ,p_{i}^{3} , ldots ,p_{i}^{n} } proper}$$

(2)

Every occasion member additionally performs the function of an election candidate, so all the inhabitants will be thought to be n constituencies, which will be represented as Eq. (3). What must be emphasised is the members of the constituency are additionally occasion members, however the logical division is completely different. The membership of every constituency is split as proven in Eq. (4).

$$C = left{ {C_{1} ,C_{2} ,C_{3} , ldots ,C_{n} } proper}$$

(3)

$$C_{j} = left{ {p_{1}^{j} ,p_{2}^{j} ,p_{3}^{j} , ldots ,p_{n}^{j} } proper}$$

(4)

Moreover, the chief of the ith occasion after computing the health of all members is famous as (p_{i}^{*}) and the set of all of the occasion leaders is represented by ({P}^{*}) as proven in Eq. (5). Equally, after the election, ({C}^{*}) regroups the winners from all of the constituencies named the parliamentarians as proven in Eq. (6), the place (c_{j}^{*}) denotes the winner of jth constituency.

$$P^{*} = left{ {p_{1}^{*} ,p_{2}^{*} ,p_{3}^{*} , ldots ,p_{n}^{*} } proper}$$

(5)

$$C^{*} = left{ {c_{1}^{*} ,c_{2}^{*} ,c_{3}^{*} , ldots ,c_{n}^{*} } proper}$$

(6)

Election marketing campaign

This stage is the core stage of the algorithm and is answerable for the situation replace of the search agent. Within the algorithm, the particular efficiency is that occasion members change their positions in keeping with the chief ({P}^{*}) of the occasion they belong to and the winner ({C}^{*}) of their constituency. As well as, they may also study from the expertise of the final election by means of a novel location replace mechanism known as latest past-based place updating technique (RPPUS), as formulated in Eqs. (7) and (8). The principle concept of RPPUS is to foretell promising areas by means of the numerical relationship between subgroup optimum resolution (occasion chief or constituency winner) and present health and former health of search agent.

$$p_{i,okay}^{j} left( {t + 1} proper) = left{ {start{array}{ll} {m^{*} + rleft( {m^{*} – p_{i,okay}^{j} (t)} proper),} hfill & {{textual content{if}}quad p_{i,okay}^{j} (t – 1) le p_{i,okay}^{j} (t) le m^{*} {textual content{ or }}p_{i,okay}^{j} (t – 1) ge p_{i,okay}^{j} left( t proper) ge m^{*} } hfill {m^{*} + (2r – 1)left| {m^{*} – p_{i,okay}^{j} (t)} proper|,} hfill & {{textual content{if}}quad p_{i,okay}^{j} (t – 1) le m^{*} le p_{i,okay}^{j} (t){textual content{ or }}p_{i,okay}^{j} (t – 1) ge m^{*} ge p_{i,okay}^{j} (t)} hfill {m^{*} + (2r – 1)left| {m^{*} – p_{i,okay}^{j} (t – 1)} proper|,} hfill & {{textual content{if}}quad m^{*} le p_{i,okay}^{j} (t – 1) le p_{i,okay}^{j} (t){textual content{ or }}m^{*} ge p_{i,okay}^{j} (t – 1) ge p_{i,okay}^{j} (t)} hfill finish{array} } proper.$$

(7)

$$p_{i,okay}^{j} left( {t + 1} proper) = left{ {start{array}{ll} {m^{*} + left( {2r – 1} proper)left| {m^{*} – p_{i,okay}^{j} left( t proper)} proper|,} hfill & {{textual content{if}}quad p_{i,okay}^{j} left( {t – 1} proper) le p_{i,okay}^{j} left( t proper) le m^{*} {textual content{ or }}p_{i,okay}^{j} left( {t – 1} proper) ge p_{i,okay}^{j} left( t proper) ge m^{*} } hfill {p_{i,okay}^{j} left( {t – 1} proper) + rleft( {p_{i,okay}^{j} left( t proper) – p_{i,okay}^{j} left( {t – 1} proper)} proper),} hfill & {{textual content{if}}quad p_{i,okay}^{j} left( {t – 1} proper) le m^{*} le p_{i,okay}^{j} left( t proper){textual content{ or }}p_{i,okay}^{j} left( {t – 1} proper) ge m^{*} ge p_{i,okay}^{j} left( t proper)} hfill {m^{*} + left( {2r – 1} proper)left| {m^{*} – p_{i,okay}^{j} left( {t – 1} proper)} proper|,} hfill & {{textual content{if}}quad m^{*} le p_{i,okay}^{j} left( {t – 1} proper) le p_{i,okay}^{j} left( t proper){textual content{ or }}m^{*} ge p_{i,okay}^{j} left( {t – 1} proper) ge p_{i,okay}^{j} left( t proper)} hfill finish{array} } proper.$$

(8)

the place (m^{*}) signifies the chief of a celebration or the winner of a constituency, (r) represents a random quantity from 0 to 1, and (t) represents the present iteration quantity.

Get together switching

The occasion switching part is especially to steadiness exploration and exploitation, which introduces an adaptive parameter (lambda) known as occasion switching charge. Every occasion member could also be chosen and switched to some randomly chosen occasion. The likelihood of switching is set by (lambda), which is initially 1 and linearly decreases to 0 as proven in Eq. (9).

$$lambda = left( {1 – frac{t}{T}} proper)*lambda_{{{textual content{max}}}}$$

(9)

Election

At this stage, the health of every candidate resolution is set and the occasion leaders and constituency winners are up to date by Eqs. (10) and (11).

$$q = mathop {{textual content{argmin}}}limits_{1 leqslant j leqslant n} fleft( {p_{i}^{j} } proper)quad p_{i}^{*} = p_{i}^{q}$$

(10)

$$q = mathop {{textual content{argmin}}}limits_{1 leqslant i leqslant n} fleft( {p_{i}^{j} } proper)quad c_{j}^{*} = p_{q}^{j}$$

(11)

Parliamentary affairs

The occasion switching part is aimed on the change of the occasion’s perspective, and the parliamentary affairs part is the change of the constituency’s perspective. The constituency winners work together with one another to enhance their health. Every constituency winner makes use of the next equation to replace its place relative to every other randomly chosen constituency. It must be famous that the motion will solely be utilized if the health of (c_{j}^{*}) turns into higher.

Fireworks algorithm

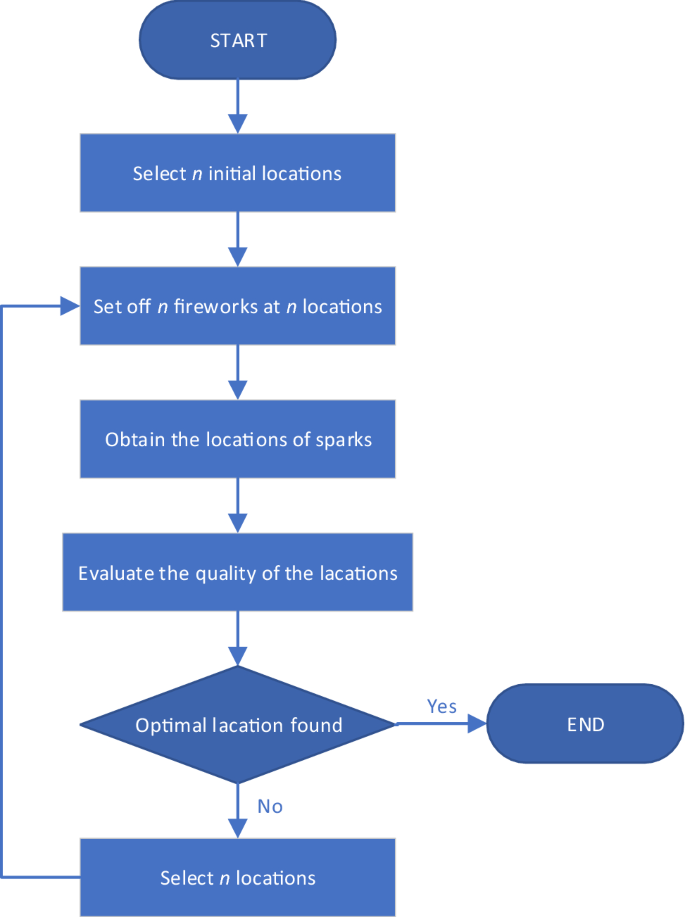
The firework algorithm (FWA) is a swarm intelligence optimization algorithm proposed lately, which is impressed by the explosion of fireworks. We normally have a good time with fireworks. When the fireworks explode, the sparks are in every single place. The explosion strategy of the fireworks will be thought to be the search habits of the search agent within the native house. The firework algorithm is predicated on this concept, and the flowchart of the firework algorithm is proven in Fig. 3.

It must be emphasised that fireworks of various qualities will produce completely different sparks once they explode. Excessive-quality fireworks will produce numerous sparks once they explode. The explosion of the fireworks kinds a circle, and the sparks are concentrated within the middle of the explosion. Conversely, a foul firework will produce fewer sparks when it explodes, and the sparks will unfold out to kind irregular shapes. From the angle of swarm intelligence algorithm, a firework is thought to be a candidate resolution. A superb firework signifies that a candidate resolution is positioned in a promising space and is near the worldwide optimum resolution. Due to this fact, extra sparks will be generated close to good fireworks to search out the worldwide optimum resolution, and the search radius is as small as potential. A foul firework signifies that the place of the candidate resolution isn’t best, so the search radius must be bigger, and the variety of sparks generated will likely be lowered accordingly.

As talked about earlier, good fireworks ought to produce extra sparks, whereas unhealthy fireworks produce fewer sparks. The calculation of the variety of sparks produced by every firework is proven in Eq. (12). Good fireworks are nearer to the worldwide optimum, so the explosion amplitude is smaller, whereas unhealthy fireworks are simply the alternative. The amplitude of explosion for every firework is outlined as Eq. (13).

$$S_{i} = hat{S} cdot frac{{y_{{{textual content{max}}}} – f({varvec{x}}_{{varvec{i}}} ) + xi }}{{mathop sum nolimits_{i = 1}^{n} (y_{{{textual content{max}}}} – f({varvec{x}}_{{varvec{i}}} )) + xi }}$$

(12)

$$A_{i} = hat{A} cdot frac{{f({varvec{x}}_{{varvec{i}}} ) – y_{{{textual content{min}}}} + xi }}{{mathop sum nolimits_{i = 1}^{n} (f({varvec{x}}_{{varvec{i}}} ) – y_{{{textual content{min}}}} ) + xi }}$$

(13)

the place (y_{{{textual content{min}}}} = {textual content{min}}(f({varvec{x}}_{{varvec{i}}} ))), (y_{{{textual content{max}}}} = {textual content{max}}(f({varvec{x}}_{{varvec{i}}} ))), (hat{S}) and (hat{A}) are constants, that are to manage the variety of explosion sparks and the dimensions of explosion amplitude, respectively.

What must be famous is FA design two methods of producing sparks, one is explosion sparks for regular search, its algorithm is proven in Algorithm 1. The opposite is Gaussian spark, which is a mutation mechanism, and its algorithm is proven in Algorithm 2.