A brand new human-based metahurestic optimization technique primarily based on mimicking cooking coaching

This half is dedicated to the introduction and mathematical modeling of the proposed algorithm referred to as the Chef-based optimization algorithm (CBOA).

Inspiration of CBOA

Cooking college students and younger cooks take part in coaching programs to enhance their cooking expertise and turn into cooks. This idea is analogous to metaheuristic algorithms, the place a number of candidate options are initialized after which improved by way of an iterative course of to find out the most effective candidate resolution as the answer to the issue on the finish of the algorithm implementation. Thus, the method of remodeling a cooking scholar right into a chef in a culinary college is a supply of inspiration for the design of the proposed CBOA.

It’s assumed {that a} sure variety of chef instructors are current in a culinary college. Every chef teacher is answerable for educating a category. Every cooking scholar can select which of those lessons to attend. The chef teacher teaches college students cooking expertise and methods. Nonetheless, chef instructors additionally attempt to enhance their expertise primarily based on the directions of the most effective chef teacher within the college and particular person workout routines. Cooking college students attempt to study and imitate the abilities of the chef teacher. As well as, cooking college students attempt to enhance the abilities they’ve discovered by way of observe. On the finish of the course, cooking college students turn into expert cooks below the coaching they’ve acquired.

Mathematical modeling of the above ideas is utilized in designing the CBOA, which is mentioned within the following subsections.

Algorithm initialization

The proposed CBOA method is a population-based algorithm whose members include two teams of individuals, particularly cooking college students and chef instructors. Every CBOA member is a candidate resolution that comprises details about the issue variables. From a mathematical viewpoint, every member of the CBOA is a vector, and the set of CBOA members will be modeled utilizing a matrix based on Eq. (1).

the place (X) is the CBOA inhabitants matrix, ({X}_{i}=left({x}_{i,1},{x}_{i,2},dots ,{x}_{i,m}proper)) is the (i)th CBOA member (candidate resolution), ({x}_{i,j}) is its (j)th coordinate (i.e., the worth of the (j)th downside variable for the (i)th CBOA member), (N) is the inhabitants measurement, and (m) is the variety of downside variables of the target operate (dimension of the issue).

The place of the CBOA members at first of the algorithm implementation is randomly initialized for (i=textual content{1,2}, dots , N textual content{and} j=textual content{1,2}, dots ,m) utilizing Eq. (2).

the place (r) is a random quantity within the interval (left[text{0,1}right]), (l{b}_{j}) and (u{b}_{j}) are the decrease and the higher bounds of the (j)th downside variable, respectively.

By inserting the steered values of every CBOA member into the variables, a corresponding goal operate worth is evaluated. Because of this, the target operate is evaluated in (N) turns (the place (N) is the variety of CBOA members) and (N) values are calculated for the target operate. These values will be represented utilizing a vector equivalent to Eq. (3).

the place (F) is the vector of values of the target operate and ({F}_{i}) is the worth of the target operate obtained for the (i)th member of CBOA, the place (i=textual content{1,2}, dots , N.)

The values of the target capabilities present important details about the standard of the candidate options. The worth of the target operate is the choice criterion for choosing the right candidate resolution. Amongst CBOA members, the member with the most effective worth for the target operate is acknowledged as the most effective member of the inhabitants and the most effective candidate resolution. In the course of the working of the algorithm, in every iteration, the members of the CBOA are up to date, and the corresponding values of the target operate are calculated. It’s, subsequently, essential to replace the most effective member in every iteration primarily based on evaluating the values of the target operate.

Mathematical modeling of CBOA

After the algorithm is initialized, the CBOA steps are steadily utilized to the candidate options to enhance them. CBOA members include a bunch of instructing cooks and a bunch of cooking college students. The replace course of for every of those teams is completely different. Primarily based on evaluating the values of the target operate, some CBOA members with higher values of the target operate are chosen because the chef teacher. Due to this fact, if the rows of the CBOA inhabitants matrix are sorted in ascending order based on the worth of the target operate (thus, the member within the first row is the most effective member), then the group of the primary ({N}_{C}) members is chosen because the group of chef instructors and the remainder group of ({N-N}_{C}) members is chosen because the group of cooking college students. The CBOA sorted inhabitants matrix and the sorted goal operate vector are laid out in Eqs. (4) and (5).

the place ({N}_{C}) is the variety of chef instructors, (XS) is the sorted inhabitants matrix of CBOA, and (FS) is a vector of ascending goal operate values. Within the matrix (XS), members from ({XS}_{1}) to (X{S}_{{N}_{C}}) characterize the group of chef instructors, and members from (X{S}_{{N}_{C}+1}) to (X{S}_{N}) characterize the group of cooking college students. The vector (FS) i consists of successively the values of the target capabilities equivalent to ({XS}_{1}) to (X{S}_{N}).

Part 1: the updating course of for group of chef instructors (replace of ({XS}_{1}) to (X{S}_{{N}_{C}}))

In a culinary college, it’s assumed that a number of chef instructors are answerable for educating cooking expertise to college students. Chef instructors comply with two methods to enhance their cooking expertise. Within the first technique, they emulate the most effective chef teacher and attempt to study the chef teacher methods. This technique demonstrates the worldwide search and CBOA exploration capabilities.

The benefit of updating the chef instructors primarily based on this technique is that the highest cooks (prime inhabitants members) enhance their expertise primarily based on the most effective chef (finest inhabitants member) earlier than they begin educating college students. Therefore, there is no such thing as a direct dependence on updating the scholars’ place solely on the bottom of the most effective member of the inhabitants in CBOA design. Moreover, this method prevents the algorithm from getting caught in native optima and causes completely different areas of the search house to be scanned extra precisely and successfully. Primarily based on this technique, a brand new place for every chef teacher is first calculated for (i=textual content{1,2}, dots , {N}_{C} ,textual content{and}, j=textual content{1,2}, dots ,m) utilizing the next equation

the place ({XS}_{i}^{C/S1}) is the brand new calculated standing for the (i)th sorted member of CBOA (that’s ({XS}_{i})) primarily based on the primary technique ((C/S1)) of updating the chef teacher, ({xs}_{i,j}^{C/S1}) is its (j)th coordinate, (BC) is the most effective chef teacher (denoted as ({XS}_{1}) within the matrix (XS)), ({BC}_{j}) is the (j)th coordinate of the most effective chef teacher, (r) is a random quantity from the interval (left[text{0,1}right]), and (I) is a quantity that’s chosen randomly throughout execution from the set (left{textual content{1,2}proper}). This new place is appropriate to the CBOA if it improves the worth of the target operate. This situation is modeled utilizing Eq. (7).

the place ({FS}_{i}^{C/S1}) is the worth of the target operate of the member ({XS}_{i}^{C/S1}.)

Within the second technique, every chef teacher tries to enhance his cooking expertise primarily based on particular person actions and workout routines. This technique represents the native search and the CBOA’s exploitation means. If every downside variable is taken into account a cooking talent, a chef teacher will attempt to enhance all of these expertise to realize a greater goal operate worth.

The benefit of updating primarily based on particular person actions and workout routines is that every member, whatever the place of different inhabitants members, seeks to find higher options close to the place the place it’s positioned. There’s a risk that higher options will be obtained primarily based on native search and exploitation, with minor modifications within the place of inhabitants members within the search house. In keeping with this idea, round every chef teacher within the search house, a random place is generated for (j=textual content{1,2}, dots ,m) utilizing Eqs. (8) to (10). If this random place improves the worth of the target operate, it’s acceptable for updating, which this situation is modeled utilizing Eq. (11).

the place (l{b}_{j}^{native}) and (u{b}_{j}^{native}) are the decrease and higher native certain of the (j)th downside variable, respectively, and the variable (t) represents the iteration counter.

the place ({XS}_{i}^{C/S2}) is the brand new calculated standing for the (i)th CBOA sorted member (i.e., ({XS}_{i})) primarily based on the second technique ((C/S2)) of chef instructors updating, ({xs}_{i,j}^{C/S2}) is its (j)th coordinate, and ({FS}_{i}^{C/S2}) is its worth of the target operate.

Part 2: the updating course of for the group of cooking college students (replace of ({XS}_{{N}_{C}+1}) to (X{S}_{N}))

Cooking college students attend culinary college to study cooking expertise and turn into a chef. Within the design of CBOA, it’s assumed that cooking college students comply with three methods to study cooking expertise. In keeping with the primary technique, every cooking scholar randomly chooses a category taught by one of many cooks, after which he’s taught cooking expertise by this chef teacher. The benefit of updating cooking college students primarily based on this technique is that there are completely different chef instructors accessible to steer them, leading to cooking college students studying completely different expertise (i.e., inhabitants members shifting to different areas of the search house) primarily based on the steering of the chosen chef teacher. Alternatively, if all cooking college students study solely from the most effective chef-instructor (all members of the inhabitants moved in direction of the most effective member), then an environment friendly international search within the problem-solving house wouldn’t be attainable. This technique is simulated within the CBOA in such a means that first for every cooking scholar, a brand new place is calculated primarily based on the coaching and steering of the chef teacher, for (i={N}_{C}+1, {N}_{C}+2, dots , N, j=textual content{1,2}, dots ,m,) utilizing Eq. (12).

the place ({XS}_{i}^{S/S1}) is the brand new calculated standing for the (i)th sorted member of CBOA (i.e., ({XS}_{i})) primarily based on the primary technique ((S/S1)) of the updating of cooking college students, ({xs}_{i,j}^{S/S1}) is its (j)th coordinate, and ({CI}_{{ok}_{i},j}) is the chosen chef teacher by the (i)th cooking scholar, the place ({ok}_{i}) is randomly chosen from the set (left{textual content{1,2}, dots , {N}_{C}proper}) (the place ({CI}_{{ok}_{i},j}) denotes the worth ({xs}_{{ok}_{i},j})).

This new place replaces the earlier place for every CBOA member, if it improves the worth of the target operate. This idea is modeled for (i={N}_{C}+1, {N}_{C}+2, dots , N) by Eq. (13).

the place ({FS}_{i}^{S/S1}) is the worth of the target operate of ({XS}_{i}^{S/S1}.)

Within the second technique, since every downside variable within the CBOA is assumed to be a cooking talent, every cooking scholar tries to study one of many expertise of the chef teacher utterly and totally imitate the chef teacher (subsequently, by “talent’’, we imply a recipe for one nice meal). This technique enhances the worldwide search and exploration capabilities of the CBOA. The benefit of this technique is that as a substitute of updating all candidate resolution variables (i.e., all cooking scholar expertise), just one variable (one talent, i.e., one recipe) modifications. It might not be essential to replace all member place coordinates to realize higher options.

Within the design of CBOA, this “talent’’ represents a sure part of a vector of cooking expertise of a randomly chosen chef teacher ({CI}_{ok}) ((kin left{textual content{1,2},dots ,{N}_{c}proper})). Therefore, the second technique is mathematically simulated in such a means that for every cooking scholar ({XS}_{i}) (members of CBOA with (i={N}_{C}+1, {N}_{C}+2, dots , N)), first one chief teacher, which is represented by the vector ({CI}_{{ok}_{i}}=left({CI}_{{ok}_{i,1}}, dots , {CI}_{{ok}_{i,m}}proper),) is randomly chosen (a member of CBOA with the index ({ok}_{i}), which is randomly chosen from the set ({1,…, {N}_{C}})), then it’s randomly chosen his (mathcal{l})th coordinate (thus a quantity (mathcal{l}) from the set (left{1,… mright},) which represents a “talent’’ of this chosen chief teacher) and by this worth ({CI}_{{ok}_{i,mathcal{l}}}) we exchange the (mathcal{l})th coordinate of the vector of the (i)th cooking scholar ({XS}_{i}) (thus, ({xs}_{i,mathcal{l}})).

In keeping with this idea, a brand new place is calculated for every CBOA cooking scholar member utilizing Eq. (14).

the place (mathcal{l}) is a randomly chosen quantity from the set (left{textual content{1,2}, dots ,mright},) (i={N}_{C}+1, {N}_{C}+2, dots , N,) (j=textual content{1,2}, dots ,m.) Then, it’s changed with the earlier place primarily based on Eq. (15) if it improves the goal worth of the target operate.

the place ({XS}_{i}^{S/S2}) is the brand new calculated standing for the (i)th sorted member of CBOA (i.e., ({XS}_{i})) primarily based on the second technique ((S/S2)) of updating cooking college students, ({xs}_{i,j}^{S/S2}) is its (j)th coordinate, ({FS}_{i}^{S/S2}) is its goal operate worth.

Within the third technique, every cooking scholar tries to enhance his cooking expertise primarily based on his particular person actions and workout routines. In truth, this technique represents the native search and the CBOA’s exploitation means. The benefit of updating cooking college students primarily based on the technique of particular person actions and workout routines is that it will increase the ability of native search and exploitation of the algorithm in reaching higher attainable options close to the found options. On this technique, much like the native search technique of chef instructors, cooking college students attempt to converge to higher options with small and exact steps. If every downside variable is taken into account a cooking talent, a cooking scholar will attempt to enhance all of these expertise to realize a greater goal operate worth.

In keeping with this idea, round every cooking scholar within the search house, a random place is generated by Eqs. (8), and (9) and a brand new place is calculated utilizing Eq. (16).

the place ({XS}_{i}^{S/S3}) is the brand new calculated standing for the (i)th sorted member of CBOA (that’s ({XS}_{i})) primarily based on the third technique ((S/S3)) of updating cooking college students, ({xs}_{i,j}^{S/S3}) is its (j)th coordinate, and (q) is randomly chosen quantity from the set (left{textual content{1,2}, dots ,mright}), (i={N}_{C}+1, {N}_{C}+2, dots , N), and (j=textual content{1,2}, dots ,m.) If this new random place improves the worth of the target operate, it’s acceptable for updating of ({XS}_{i}), which is modeled by Eq. (17).

the place ({FS}_{i}^{S/S3}) is the worth of the target operate of ({XS}_{i}^{S/S3}.)

Repetition course of, pseudocode, and flowchart of CBOA

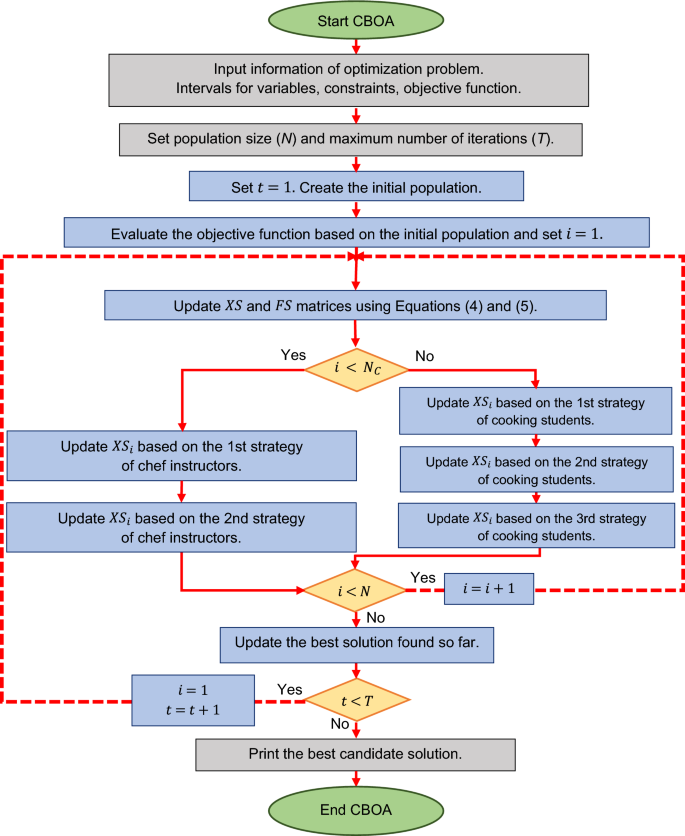
A CBOA iteration is accomplished by updating all members of the inhabitants. The CBOA enters the subsequent iteration with these new statuses, and the teams of chef instructors and cooking college students are respecified. The inhabitants members are up to date primarily based on the implementation of the CBOA steps based on Eqs. (4) to (17) till the final iteration of the algorithm. After reaching the utmost worth of the iteration variable CBOA, the most effective candidate resolution obtained throughout the implementation course of is offered as the answer to the issue. Varied steps of CBOA implementation are offered within the type of a flowchart in Fig. 1 and its pseudocode in Algorithm 1.

Computational complexity of CBOA

On this subsection, the computational complexity of the CBOA is analyzed. Making ready and initializing the CBOA for an optimization downside, with the variety of resolution variables (m), has a computational complexity of (O(Nm)), the place (N) is the variety of CBOA members. Updating the group of chef instructors in two methods has a computational complexity equal to (O(2{N}_{C}mT)), the place T is the utmost variety of CBOA iterations and ({N}_{C}) is the variety of chef instructors. Updating the scholar cooking group in three methods has a computational complexity equal to (O(3 (N-{N}_{C}) mT)). Thus, the whole computational complexity of CBOA is the same as (O(m(N + 2{N}_{C}T + 3 left(N-{N}_{C}proper)T ))).