Dynamic algorithm for health perform significantly improves the optimization effectivity of frequency selective floor for higher design of radar

The affect of weight choice on optimization effectivity

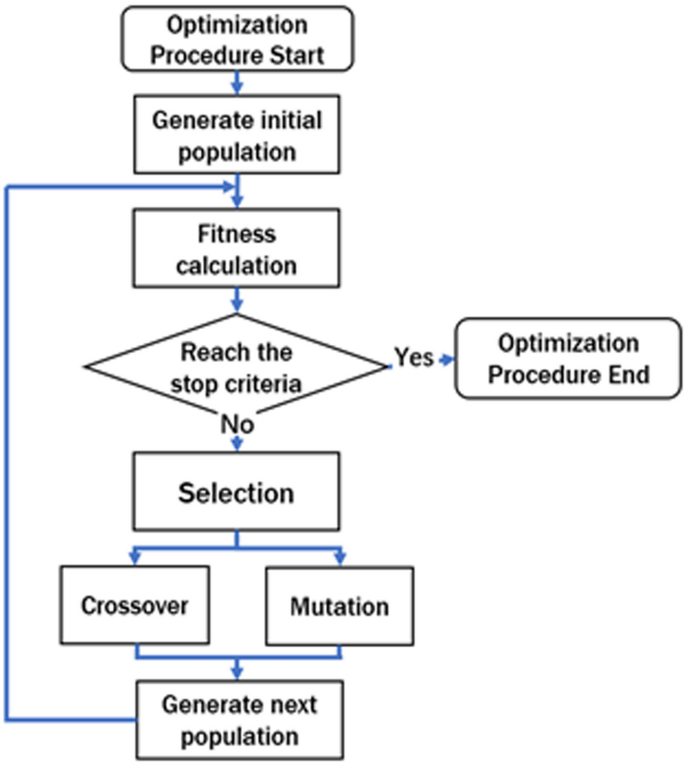
In our work, Finite-Distinction Time-Area (FDTD) is used to unravel the electromagnetic traits of FSS, and GA is utilized to optimize absolutely discretized FSS buildings. The GA procedures are proven in Fig. 1. Right here, the health perform is used to guage the excellence of people of every inhabitants era. Be aware that we used binary coding to specific FSS buildings on this paper.

Flowchart of genetic algorithm optimization. Be aware that on this paper, we used binary coding to specific FSS buildings. Choice, crossover, and mutation are the basic operations in GA.

The analysis of the FSS construction high quality consists of middle frequency, primary lobe energy, and SLL, which we label as V₁(X), V₂(X), and V₃(X). The three indexes may be unified into vector kind, that’s, V(X) = (V₁(X), V₂(X), V₃(X)). Then the whole health perform of vector kind may be expressed as:

Right here,

(f_{i} left( X proper)) is the sub health perform on the sub goal i. (O_{i}) is the design goal worth of sub goal i. For the middle frequency, the nearer the calculated worth of (X^{left( 1 proper)}) is to the goal worth, the higher the efficiency is. The standard of primary lobe energy and SLL will increase monotonously with its worth. The three sub goal capabilities are unified to the shape that the smaller the worth is, the higher the FSS efficiency is. On this paper, we set the goal values (O_{1}) to be 8.5 GHz,( O_{2}) starting from 0.8 to 0.95 and (O_{3}) starting from—15 to—28 dB. With a purpose to examine the general high quality of two particular person FSS buildings straight, linear weighting technique is launched with the perform of

Right here, (w_{1} ,w_{2} ) and ( w_{3}) are the weights of three sub targets, respectively. Because the selection of weight components performs a key position in optimization effectivity, we in contrast two totally different generally used choice strategies: Delphi technique^19,20 and stepwise regression technique^21,22.

The Delphi technique is a suggestions correction technique to regulate the weighting components. Beginning with a random weight mixture, the weighting components will likely be redetermined artificially in response to the problem in the direction of the person optimum targets in each 1000 generations of GA. Then, the load components will likely be adjusted to convergence through the course of, and the ultimate weights will typically be applicable for optimization¹⁹.

Desk 1 is an occasion of weighting issue choice. After each 1000 generations as a cycle of the Delphi technique, a brand new weight mixture was determined manually by evaluating optimization levels of sub-objectives. In Desk 1, we are able to get that the suitable weight mixture varies all through the GA evolution. The burden of middle frequency decreases step by step; in distinction, the load of SLL had a slight increment. The ultimate weight we get is (0.18, 0.36, 0.46), of which middle frequency has the least weight whereas SLL has essentially the most. We design three various teams of efficiency necessities for additional research, from the tough to realize (strict necessities) to simple to realize (unfastened necessities). They’re labelled as goal degree 1, goal degree 2 and goal degree 3, with corresponding sub-targets ([(O_{1} ,O_{2} ,O_{3})]) of [8.5 GHz ± 0.2 GHz, 0.95, − 25 dB], [8.5 GHz ± 0.3 GHz, 0.92, − 20 dB] and [8.5 GHz ± 0.5 GHz, 0.90, − 15 dB] respectively. The ultimate weight ratios are proven in Desk 2 with the Delphi technique.

Desk 2 exhibits that the Delphi technique’s weight issue differs for various goal ranges. Particularly, the stricter necessities (from 3 to 1), the load of middle frequency will increase from 0.120 (for degree 3) to 0.147 (for degree 2) to 0.180 (for degree 3). The other monotonous pattern can be proven within the weight ratio of the principle lobe energy, the place the worth decreases from 0.437 for degree 3 to 0.363 for degree 1. Nonetheless, the load coefficient of SLL doesn’t change monotonously with the rising optimization issue. The burden coefficient of SLL is comparatively the biggest, which the utmost worth reaching 0.45. The experimental outcomes of the Delphi technique on three totally different goal ranges present that the choice of one of the best weight issue is determined by the goal situations, and the middle frequency is less complicated to optimize. On the identical time, SLL is tougher and desires a better weight.

The stepwise regression technique is an incomplete induction technique that compares the effectivity of various weight units to get the suitable weight ratio shortly. We introduce this technique to know the affect of weight choice on optimization effectivity beneath totally different goal ranges. The variety of required generations to realize the convergent weight issue set at totally different mounted weight components of middle frequency (w_{1}) values primarily based on three totally different goal ranges (the identical because the Delphi technique). The required era quantity for the optimization shouldn’t be solely associated to (w_{1}), but additionally associated to the goal degree. For goal degree 1, one of the best weight mixture that makes use of the least era to realize the goal is (0.2, 0.4, 0.4), which took 967 generations. In distinction, weight mixture (0.8, 0.1, 0.1) took 2752 generations that are essentially the most inefficient. Identical for goal degree 2, one of the best weight mixture is (0.2, 0.3, 0.5), which took 509 generations, whereas the worst weight mixture (0.7, 0.2, 0.1) took 1448 generations. For goal degree 3, one of the best weight mixture is (0.1, 0.7, 0.2), which took 280 generations, whereas the worst weight mixture (0.5, 0.4, 0.1) took 613 generations. Due to this fact, we are able to conclude that the convergent weight issue set depends on the goal necessities, i.e., totally different goal necessities akin to totally different weight issue units. As well as, the optimum weight issue set is carefully associated to the worth of every sub-target situation. And in greater necessities, the SLL degree ought to have a better weight.

In conclusion, the above two weight choice strategies, Stepwise regression makes use of mounted weight, which proved to be inefficient within the optimization. Furthermore, the Delphi technique shouldn’t be a real-time weight resolution technique. It took loads of generations of GA to find out a comparatively environment friendly weight mixture. The energetic weight all the time lags behind one of the best weight for generations. This may trigger adversarial results on optimization effectivity. Final however not least, the Delphi technique wants handbook changes to the load each 1000 generations; it isn’t handy for an automated algorithm to enter every so often.

Dynamic algorithm for health perform

To enhance the general optimization effectivity, we suggest a dynamic algorithm for health perform which might alter the load ratio in response to the continual evolution of the inhabitants. To start with, it’s essential to guage the optimization issue of every sub-objective. There’s a discrete distribution among the many inhabitants in every GA era for every sub-objective. Thus, we are able to decide the statistical high quality of every era by calculating the distinction between a reference worth (each particular person in among the many era) and the goal worth. For a person FSS construction within the era, a extra minor distinction signifies higher efficiency within the corresponding sub-objective. Because the termination situation is to acquire just one particular person FSS construction that satisfies all of the three required targets, solely one of the best particular person in a single era inhabitants is required to fulfill the usual, slightly than the general common efficiency. Due to this fact, on the mounted common efficiency of the inhabitants, extra important dispersion reveals a better likelihood for one of the best particular person to fulfill the requirement. A inhabitants with immense potential ought to have main common efficiency and huge dispersion in our GA course of. Right here, we introduce the optimization issue issue Q_n to guage the target n.

Right here, (O_{n}) is the goal sub-objective worth. (ref_{n} left( i proper)) is the reference worth of the inhabitants degree within the ith era, which is the common worth of the inhabitants. (std_{n} left( i proper)) is the usual deviation of all people in era i of sub-objective n, which signifies the diploma of dispersion of the era inhabitants.

The numerator half in Eq. (6) is the distinction between the reference worth and the goal worth of all people within the ith era, representing the diploma of optimization on this sub-objective. Suppose the reference worth is throughout the goal vary, indicating that the inhabitants of this era has been optimized on this sub-objective. In that case, the load needs to be set to 0 as a result of there isn’t a have to put the load on this sub-target. Suppose there’s a distinction between the reference worth and the goal worth, indicating that the inhabitants nonetheless has potential for optimization on this sub-objective. In that case, the load needs to be set to larger than 0. The bigger the distinction is, the larger the load needs to be set. Due to this fact, the problem issue (Q_{n}) is proportional to absolutely the worth of the distinction between the sub-objective worth and the inhabitants reference worth.

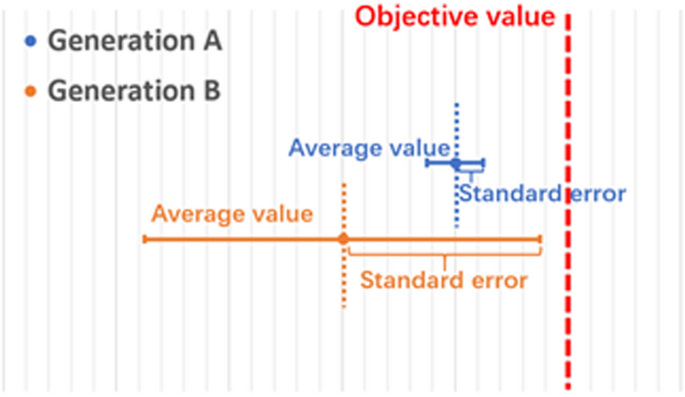
The denominator is the usual deviation of all people within the ith era on the sub-objective n. The usual deviation represents the dispersion of people on this era. The smaller the dispersion is, the extra concentrated the values of all people within the inhabitants are. As mentioned, the likelihood of getting a person to succeed in the target is positively correlated to the inhabitants’s commonplace deviation within the situation that the reference worth is mounted. For example, Fig. 2 compares two populations at two totally different generations among the many GA evolution, the place the common worth of B is decrease than that of A, however the usual deviation of B is larger than that of A. On this case, the worth of one of the best particular person in inhabitants B is nearer to the goal worth than that of inhabitants A. On this case, the problem issue (Q_{n}) for inhabitants B will likely be smaller than for inhabitants A. It exhibits that the problem issue (Q_{n}) is inversely proportional to the usual deviation of the inhabitants. In conclusion, the dynamic algorithm we proposed compares the distribution of GA people over every sub-target and the common distance from the goal, which can be utilized as an applicable expression for the problem of optimization. Accordingly, the load mixture within the dynamic algorithm for health perform for subsequent GA era is adjusted to maximise the computing energy and effectivity.

Comparation between two populations at two totally different generations among the many GA evolution. Era B has a decrease common worth however a bigger commonplace error whereas era A is within the reverse scenario. On this case, era B is taken into account to be in additional optimized situation that ought to assign a smaller weight.

It needs to be identified that (Q_{n} left( i proper)) is a dimensionless parameter, which might categorical the optimization issue of every sub-objective in a sure era. After normalization of (Q_{n} left( i proper)), we are able to get the load values (w_{1} ,w_{2} ) and ( w_{3}).

By substituting Eq. (7) into Eq. (5), we are able to get the type of whole health perform of era i.

Equation (8) is the brand new dynamic algorithm for the health perform designed on this paper. With this health perform, the optimization course will likely be tuned primarily based on every era by robotically altering the load components for higher choice of the people to take part within the GA operation and enhancing general optimization effectivity.

To confirm the effectiveness of the brand new dynamic algorithm, we examine it with the mounted weighted health perform and Particle Swarm Optimization (PSO) algorithm for FSS design²³. The preliminary inhabitants was the identical people generated randomly for the three strategies. The mounted weight ratios are set to be fixed (0.3, 0.4, 0.3), which is a comparatively applicable mixture in most conditions.

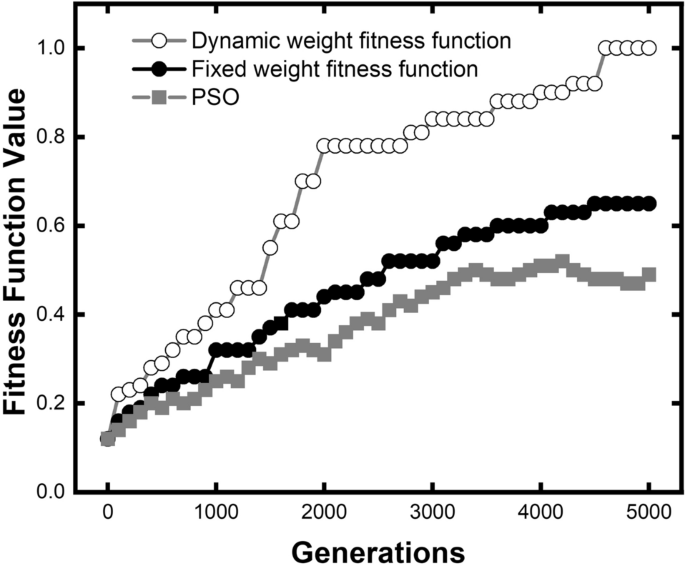
As proven in Fig. 3, the generation-evolution of the health values relative to the goal worth are in contrast primarily based on two totally different weight capabilities: the dynamic weight health perform (hole circle dotted grey line), the mounted weight health perform (strong circle dotted black line), and the PSO (strong sq. dotted grey line). The health worth of PSO algorithm relies on the parameters of the optimum particular person of every era (iteration) in and calculated by Eq. (8). The health worth on the 5000th era of dynamic algorithm was taken as 1.00 to normalize. The optimization of the mounted weight health perform progresses steadily alongside the entire GA course of. The optimization progress of the dynamic algorithm is advanced. The health perform worth raises quickly in a number of phases. Within the first 1000 generations, two health capabilities are began from the identical preliminary populations. Three sub-objectives are removed from the goal worth, making the load of the three sub-objectives shut to one another within the dynamic algorithm. There’s a slight distinction between the black and grey strains within the first 800 generations. The dynamic algorithm had a slight benefit in optimization effectivity. As soon as it involves the second part (800–1500 generations), the middle frequency is sort of absolutely optimized after the primary 800 generations. The dynamic algorithm for health perform can reassign weights in response to optimization issue, decreasing the load of middle frequency and rising the opposite two sub-objectives. However, the mounted weight technique is not going to change the load mixture. This makes the optimization effectivity of dynamic algorithm far exceed the mounted we till 1900 era. After the 1900 era, three sub-objectives are all at a comparatively excessive degree for dynamic algorithm, so the optimization effectivity falls again to a gradual charge. At 4500 era, the dynamic algorithm had an additional leap, however it’s close to the cease standards.

Comparability of complete optimization effectivity between dynamic algorithm for health perform and glued weight health perform. Dynamic algorithm has a bonus in general optimization effectivity on the early stage of GA course of.

General, it solely takes 1800 generations for the dynamic weight health perform to realize the identical wonderful efficiency (0.6 health worth in Fig. 3), which solely makes use of 32% generations of the mounted weight. It signifies that the optimization effectivity is 213% greater than the mounted weight.

Completely different from two curves utilizing GA, the health worth of PSO grows at a comparatively fixed charge and is trapped in native convergence on the 3500th iteration. The ultimate health worth for PSO is 0.49. For our dynamic algorithm, it took solely 1600 generations to realize the identical efficiency. In iteration numbers, the dynamic algorithm is thrice extra environment friendly than PSO. In consequence, algorithm is extra resistive to native convergence in contrast with PSO.

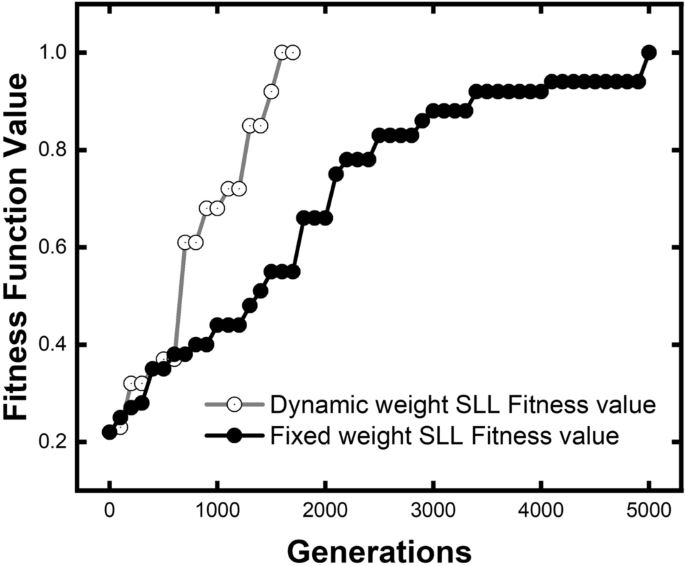
Because the SLL is the vital property to optimize, we illustrate the optimization effectivity of our dynamic algorithm of SLL individually in Fig. 4. The health worth on the 5000th era of mounted weight algorithm was taken as 1.00 to normalize. Within the first 750 generations, two health capabilities work nearly the identical on SLL for the reason that optimization is targeted on middle frequency. When the middle frequency is near the goal worth, the optimization-focus of the dynamic algorithm step by step inclined to SLL, which ends up in a form improve of the optimization charge between era 750–1800.

Comparability of SLL optimization effectivity between dynamic algorithm for health perform and glued weight health perform. Dynamic algorithm has a major benefit in SLL optimization effectivity on the early stage of GA course of.

In contrast with the mounted weight perform, the brand new health perform makes use of solely 24% of generations to succeed in the goal worth, indicating that the optimization effectivity is 315% greater. Our distinctive technique exhibits thrilling potential within the optimization of SLL. In our GA course of with the brand new dynamic algorithm, the extra problem to optimize sub-target SLL is absolutely thought-about by analyzing the inhabitants degree. Thus, SLL is granted an affordable weight that’s greater than the opposite two sub-objectives. Because of this, SLL improved optimization effectivity by utilizing a dynamic algorithm.

The above computations show that the dynamic weighted health perform has greater optimization effectivity than the mounted weight health perform. Within the numerator a part of (Q_{n}), the reference worth is chosen as (avg_{n}). The issue method of (Q_{n} ) is

It nonetheless requires extra research on whether or not (avg_{n}) is one of the best parameter to symbolize the era degree. Based on the optimization mechanism of the genetic algorithm, the termination situation is that one of the best particular person in a era reaches the goal worth. Due to this fact, one of the best particular person or one of the best worth in a sub-objective can be utilized as a reference worth to characterize the diploma of era optimization. On this scenario, we are able to get a problem coefficient (Q_{n}) with most worth (max_{n} left( i proper)) because the reference worth

However, the common worth shouldn’t be an entire expression of the era degree due to the discreteness of the people within the sub-objective. Median worth (median_{n} left( i proper) ) and the worth of golden part level ( 49th_{n} left( i proper)) (forty ninth within the case of 128 people) are typical statistics values which might remove the affect of maximum values. They might be a greater illustration of inhabitants degree on this case.

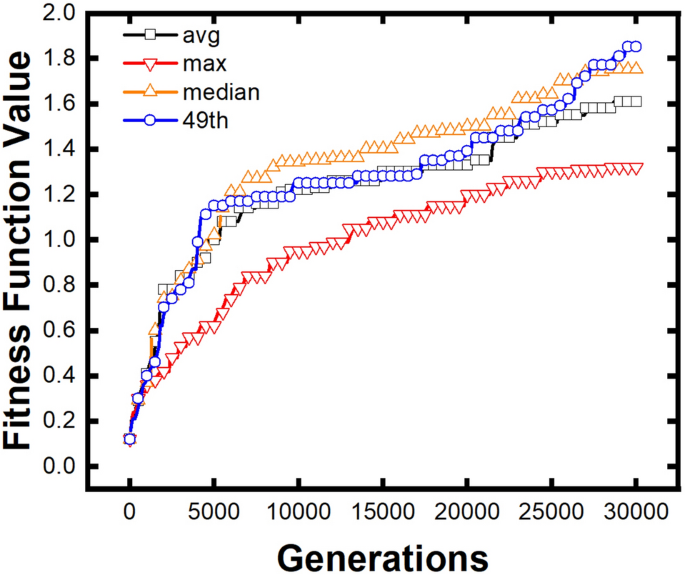
We introduce all of the above expressions of issue coefficient in Eqs. (9)–(12) to optimize the identical preliminary inhabitants. The optimization effectivity is in contrast in Fig. 5. Right here, values are normalized to the 30,000th era of the common reference worth (the black line), which is used as the first comparative perform. As proven in Fig. 5, reference worth as most worth (purple line), median worth (orange line), and as golden part worth (blue line) can all optimize FSS construction successfully.

Comparability of the optimization effectivity between totally different reference values. Utilizing the median worth and golden part factors have greater optimization effectivity, whereas utilizing the common worth is much less environment friendly, and utilizing the utmost worth is least environment friendly.

The health worth on the at 30,000th era utilizing common reference values was taken as 1.00 to normalize. There isn’t any apparent distinction between the median reference worth and the golden part reference worth towards the common reference worth within the first 4700 generations. The median health worth quickly rose from 4700 to 6500 generations and maintained its benefit in optimization effectivity till the top of the calculation. The golden part worth health perform had two speedy rises, from 4000 to 5000 generations and from 26,000 to 27,000 generations, and it has one of the best consequence at 30,000 era. The purple line represents the utmost reference worth of method (10). The optimization progress is clean however step by step decrease than the three different reference values. It needs to be famous that the relative worth is barely 0.385 within the 5000th era when introducing the utmost reference worth. It’s about 40% decrease than that utilizing the common worth, which is 0.621. The health worth is 0.633 when utilizing median reference worth in 5000th era, which is 2% greater than the health perform utilizing common worth. The health worth is 0.714 when utilizing golden part reference worth in 5000th era, which is 15% greater than the health perform utilizing common worth. Contemplating the extent of the 30000th era, the health worth of the utmost reference worth continues to be the bottom, which is 0.820. The health values of utilizing the median and golden part factors are greater, that are 1.087 and 1.149, respectively.

Based on the experimentation, it may be concluded that utilizing the median worth and golden part factors have greater optimization effectivity, whereas utilizing the common worth is much less environment friendly, and utilizing the utmost worth is least environment friendly.

The inhomogeneous distribution of SLL can clarify the effectivity distinction between median and common health perform. Based on the traits of the genetic algorithm, one of the best people of a era can be much better than others, particularly in SLL. Therefore, the arithmetic imply worth of a era in SLL could also be greater than the inhabitants degree. Median worth and golden part worth rely upon the people rating of sub-objectives, no matter excessive good or dangerous people. In conclusion, the common worth is an effective reference for sub-objectives with a comparatively uniform distribution. Nonetheless, for instances with excessive distribution, particularly in GA, the median or golden part reference worth will carry out higher.

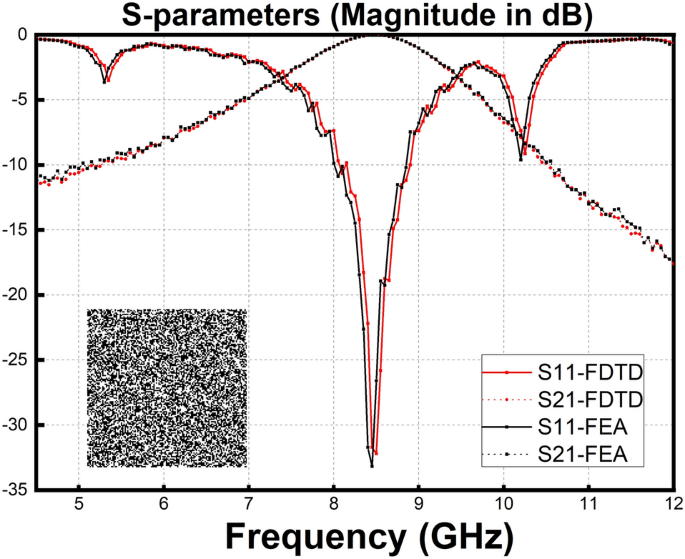
In Fig. 6, the sample and S-parameters of essentially the most optimum results of Fig. 5 are proven. Finite aspect evaluation (FEA) technique is used as a verification of the FDTD technique primarily used within the paper. The S-parameter curves obtained by the 2 strategies have trivial distinction. The middle frequencies are 8.49 GHz and eight.47 GHz, respectively for FDTD and FEA that are each follow the target worth we now have set..

The sample and S-parameters of essentially the most optimum consequence. FDTD and FEA technique are used to confirm the ultimate consequence. Based on the S parameter curve, one of the best particular person of the 30,000th era of GA course of utilizing golden part level reference worth has a middle frequency close to 8.50 GHz, which is follow the target worth we now have set.

To elucidate the inefficiency of most reference worth. We will evaluate the formulation. The denominator a part of method (9) is similar as that of method (10), and the issue inflicting the effectivity distinction is the numerator components of the formulation. On this paper, we think about the case of a selected inhabitants case n with i sub-objectives. (avg_{n} left( i proper)) is unquestionably lower than (max_{n} left( i proper)). Within the case of inadequate optimization, (avg_{n} left( i proper)) and (max_{n} left( i proper)) are each lower than (O_{n}). Due to this fact, the numerator a part of the Eq. (9) is bigger than that of Eq. (10), and the distinction is determined by the dispersion diploma of the inhabitants on this sub-objective. Based on the traits of the frequency selective floor, the dispersion diploma of the sidelobe degree is larger than the middle frequency and the principle lobe energy, so the distinction ratio of the numerator on the sidelobe degree will likely be larger than the middle frequency and the principle lobe energy, the load of sidelobe degree obtained by issue method (10) is lower than that obtained by utilizing the problem method (9).

To confirm the above conclusion, two generations of the inhabitants have been randomly chosen, that are the 4768th era of the common reference worth and the 15673rd era of the median reference worth. As proven in Desk 3, the weights of three sub-objectives have been obtained via Eqs. (9) and (10).

For 2 generations of the inhabitants, the load of sidelobe degree in most reference worth is considerably decrease than that in common reference worth. The lower of optimization effectivity in most reference worth additionally verifies the conclusion obtained by the Delphi technique: the optimum weight issue for SLL, which is tougher to optimize must be greater than different sub-objectives.