Optimization methodology and experimental analysis on angle adjustment scheme of angle adaptive rescue robotic

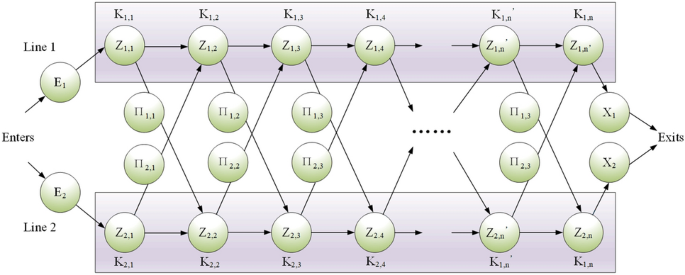
The ballast water allocation strategy of rescue robots is a multistage decision-making downside, which is a steady dynamic course of. The benefit of dynamic programming algorithms is that they are often mixed with associated engineering issues to divide a steady course of into a number of interrelated phases. Through the answer course of, the optimization outcomes of the earlier stage are repeatedly used to hold out the optimization answer of the subsequent stage. The ballast water allocation downside of rescue robots is considered a steady downside, and a dynamic programming algorithm is used to resolve the optimum choice^{22,23,24,25,26}. The conceptual diagram of the dynamic programming algorithm is proven in Fig. 7.

Dynamic programming multistage choice idea diagram.

Determine 7 clearly exhibits the benefits and traits of the algorithm within the face of multistage multiattribute decision-making issues, that’s, in stage Okay_n,m below completely different states Z_n,m, by choosing completely different decision-making methods Π_n,m within the stage, the subsequent optimum stage Okay_n+i,m+j, and the worldwide optimum answer are attain.

In abstract, this analysis primarily research the method of ballast water allocation. By actively “salvaging” drowning individuals or aiding them to climb a rescue community, a lifting operation is carried out. Through the rescue course of, a sure lifting peak interval is used as a stage variable to make real-time dynamic choices and destroy or stabilize the posture or stability of the robotic within the water, scale back the water regulation and distribution, enhance the ballast water allocation effectivity, decrease the water tank inlet/discharge time because the optimization objective, and take the stage area, state area, choice area and state transition equation to determine a mathematical mannequin for the optimum answer of the inlet/discharge of ballast water tank primarily based on a dynamic programming algorithm.

Stage area

The stage area is normally a finite, infinite or steady set of factors. The finite stage area may be outlined because the set of Okay as:

The infinite set of stage areas is:

State area

The state refers back to the description of the system after it decides at a sure stage. This examine defines all of the states of the system as Z, which is known as the state area. Any state ({textual content{Z}}_{{upkappa }}) at any stage N belongs to Z, denoted as ({textual content{z}}_{{textual content{ok}}} in {textual content{Z}}). Due to this fact, the state area may also be expressed as:

The choice-making stage set Okay of the method is split into N + 2 phases primarily based on the lifting peak interval of every phase. For comfort of calculation, the ballast water tanks on each side are considered normal cuboids. The port and starboard sides are represented by the letters P and S, respectively, and the water stage peak of every ballast tank on each side at completely different decision-making phases is taken because the state set. Then, the state area is represented as (Z_{Okay}^{P}) and (Z_{Okay}^{S}), respectively, which is collectively known as (Z_{Okay}^{P,S}), that’s:

the place ({{d}}_{{{{Ki}}}}^{{{P,S}}}) represents the typical water stage within the ith ballast tank on the port and starboard sides of the robotic below the Nth stage, and ({{d}}_{{{{Ki}}}}^{{2{P,S}}}) may be divided into (d_{{Okay{textual content{i}}}}^{P}) and (d_{{Okay{textual content{i}}}}^{S}).

Motion area

The motion area is normally a random decision-making alternative that describes a sure state from a sure stage Okay to the subsequent stage Okay + 1^27,28. Based on the precise robotic working precept, the water stage change development of every ballast tank at completely different decision-making phases on each side may be outlined because the uncertainty motion area D:

the place (D_{ki}^{P,S}) represents the random motion set of the ith ballast tank on the port or starboard facet of the robotic within the Nth stage; ri corresponds to the rise within the water stage; lr corresponds to the lower within the water stage; and st corresponds to the extent of the water stage.

Determination area

When making a random motion choice, it’s vital to specific the quantified motion impact in mathematical type. Due to this fact, the motion units of the port and starboard are outlined as (D_{Okay}^{P} left( {Z_{Okay}^{P} ,Z_{Okay}^{P} } proper)) and (D_{Okay}^{S} left( {Z_{Okay}^{S} ,Z_{Okay}^{S} } proper)), respectively, which may be collectively known as (D_{Okay}^{P,S} left( {Z_{Okay}^{P,S} ,Pi_{Okay}^{P,S} } proper)), that’s:

the place (D_{Okay}^{P,S} left( {Z_{Okay}^{P,S} ,Pi_{Okay}^{P,S} } proper)) represents the decision-making impact of the i-th ballast tank on the port and starboard sides within the N-th stage below motion area D; (Pi_{Okay}^{P,S}) represents the change within the common water stage, which is known as the technique area.

The port and starboard sides are denoted as (Pi_{Okay}^{P}) and (Pi_{Okay}^{S}), respectively, collectively known as (Pi_{Okay}^{P,S}), that’s:

the place (Delta d_{Ki}^{P,S}) may be divided into (Delta d_{Ki}^{P}) and (Delta d_{Ki}^{S}), the place (Delta d_{Ki}^{P}) represents the typical water stage peak change of the ith ballast tank below the Nth stage on the port facet, and (Delta d_{Ki}^{S}) represents the typical water-level peak change of the ith ballast tank below the Nth stage on the starboard facet.

State transition operate

A state transition operate is constructed to symbolize the purposeful course of expression when state (Z_{Okay}) reaches the subsequent state (Z_{Okay + 1}) below the affect of an motion (D_{Okay}) and a choice area (Pi_{Okay}^{P,S}). The transition state (Z_{Okay + 1}) may be obtained in keeping with the state transition operate F, which may be expressed as (F_{Okay}^{P} left[ {Z_{K}^{P} ,D_{K}^{P} left( {Z_{K}^{P} ,Pi_{K}^{P} } right)} right]) and (F_{Okay}^{S} left[ {Z_{K}^{S} ,D_{K}^{S} left( {Z_{K}^{S} ,Pi_{K}^{S} } right)} right]), collectively known as (F_{Okay}^{P,S} left[ {Z_{K}^{P,S} ,D_{K}^{P,S} left( {Z_{K}^{P,S} ,Pi_{K}^{P,S} } right)} right]), that’s:

the place (F_{Okay}^{P,S} left[ {Z_{K}^{P,S} ,D_{K}^{P,S} left( {Z_{K}^{P,S} ,Pi_{K}^{P,S} } right)} right]) is the overall expression of the state transition operate of the port and starboard N-th stage. Amongst them, (Z_{1}^{P} = d_{0}^{P}) and (Z_{1}^{S} = d_{0}^{S}).

Expectation operate

The expectation operate is the quantitative operate used to measure and consider the benefits and downsides of the chosen technique.

On this examine, (S_{Okay}^{P,S} left[ {Z_{K}^{P,S} ,D_{K}^{P,S} left( {Z_{K}^{P,S} ,Pi_{K}^{P,S} } right)} right]) is used to symbolize the index when the choice made in state (Z_{Okay}^{P,S}) is (D_{Okay}^{P,S} left( {Z_{Okay}^{P,S} ,Pi_{Okay}^{P,S} } proper)) within the Nth stage; that’s, the ballast time within the Nth stage is:

the place (S_{1}^{P,S} left[ {Z_{1}^{P,S} ,D_{1}^{P,S} left( {Z_{1}^{P,S} ,Pi_{1}^{P,S} } right)} right]) represents the entire anticipated worth below a sure motion choice within the first stage of the port and starboard throughout the angle preadjustment course of earlier than rescue; (S_{Okay}^{P,S} left[ {Z_{K}^{P,S} ,D_{K}^{P,S} left( {Z_{K}^{P,S} ,Pi_{K}^{P,S} } right)} right]) represents the entire anticipated worth below the motion choice from the second stage to the N + 1th stage of the spatial angle adjustment within the rescue course of; (S_{N + 2}^{P,S} left[ {Z_{N + 2}^{P,S} ,D_{N + 2}^{P,S} left( {Z_{N + 2}^{P,S} ,Pi_{N + 2}^{P,S} } right)} right]) represents the entire anticipated worth below the N + 2th stage motion choice within the publish salvage drainage course of; (p) is the density of ballast water; and (m_{i}^{P,S}) represents the underside space of the ith ballast tank on the port and starboard sides.

State-action Q-value operate

In abstract, the Bellman equation expression of the state-action Q-value operate of all phases may be derived in keeping with the above calculation course of and expressed as a recursive description as follows:

The optimum Q-value operate is outlined as (Q_{Okay}^{P,S}) and expressed because the anticipated sum of stage N:

Then, the optimum state-action Q-value operate Bellman equation expression is expressed as:

The utmost anticipated worth is obtained when the optimum Q-value operate is decided. Thus, the motion technique can also be optimum, which satisfies:

This motion coverage, (D^{ * } left( {Z,{Pi }} proper)), is alleged to be grasping for the Q-value operate. Due to this fact, if the optimum (Q^{ * P,S} left[ {Z,Dleft( {Z,{Pi }} right)} right]) worth may be decided, the grasping motion may be calculated, and the optimum motion technique (D^{ * } left( {Z,{Pi }} proper)) may be obtained.

Due to this fact, in keeping with the derivation of the above expression, the optimum motion methods of the port and starboard sides may be simply obtained, which may be recursively expressed as:

Contemplating the primary two phases of the port facet for example, the optimum motion technique of the port facet:

Thus, the optimum motion technique of every stage is obtained recursively in keeping with the optimum technique of the port facet is:

That’s, the optimum coverage set below the port optimum motion is:

The optimum deployment plan for the port facet is then obtained. Equally, the optimum technique set for the starboard facet is derived as follows:

Then, the optimum technique set of the general system may be simply obtained as:

Lastly, a calculation movement chart of the optimum allocation scheme of ballast water for attitude-adaptive rescue robots primarily based on a dynamic programming algorithm may be obtained, as proven in Fig. 11.